今天学习了@Carl哥的背包问题，觉得有必要自己总结一下，加深理解，链接如下：

0-1背包理论基础（一）
0-1背包理论基础（二）

01背包

有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

暴力解法

假如我们并没有学习了解过动态规划，这道题该如何解决呢？

在物品总重小于等于w的前提下，计算出所有物品的组合的价值，选择最大的价值。这是非常典型的回溯。

所以时间复杂度为$O(2^n)$；在借助操作系统栈的前提下，空间复杂度为$O(n)$

暴力解法妥妥超时

二维dp数组

使用动规五步曲分析：

1. 明确dp数组以及下标的含义

为啥使用二维数组作为dp数组呢？因为一个维度用来遍历物品，一个维度用来遍历背包。遍历物品比较好理解，遍历背包呢？我理解的是，背包容量为w，那背包中装的物品重量只要小于等于w就可以了，所以从0开始遍历装了每种重量的情况。

dp[i][j]的含义是：在每种容量j中，从下标[0,i]中任取物品，使背包中物品的价值最大。

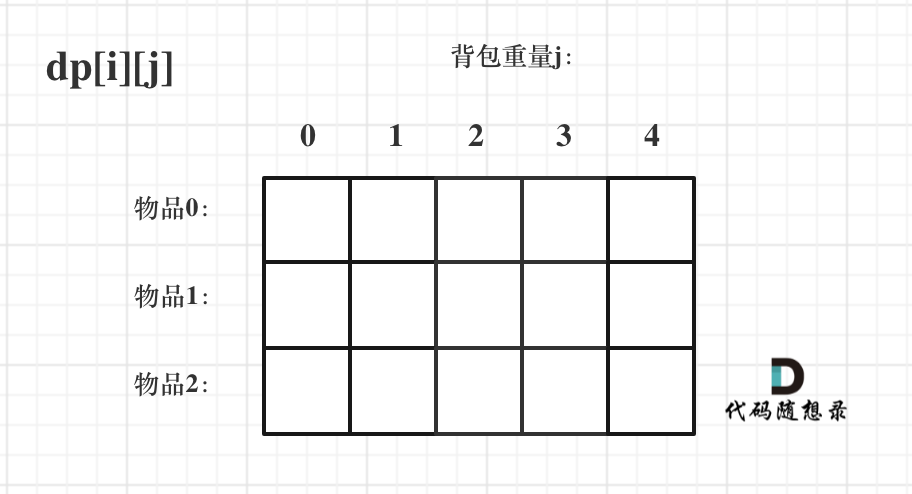
2. 递推公式推导

从两个方向推导递推公式：

不放物品i：物品i的重量weight[i] > 背包容量j，所以此时的背包中的最大价值和前一个最大价值是一样的，即：dp[i-1][j]；（位置为正上方）
放物品i：物品i的重量weight[i] <= 背包容量j，此时背包中的最大价值为dp[i-1][j-weight[i]] + value[i]；（位置是左上方，不一定是左上角，可能是[0, 左上角]中的任意位置）
一定要明确：这里的j不是个表面意义上的索引，它代表的是背包的容量。这个[j-weight[i]]表示的是：背包需要留出这个物品i的容量才可以放物品i。

综上：

if(j < weight[i])   // 容量j < 当前物品的重量，即当前物品无法放进背包
    dp[i][j] = dp[i-1][j];
else                // 当前物品可以放进背包
    dp[i][j] = Math.max(dp[i-1][j], dp[i-1][j-weight[i]]+value[i]);

3. dp数组初始化

背包容量为0时，啥也放不下，所以dp[0][j] = 0;
看物品0，放进哪个容量都是那么多的价值，所以从容量1(容量0已经初始化成0了)开始遍历：
if(j >= weight[0]) dp[0][j] = value[0];

别的不需要初始化，因为都能通过递推公式计算出来，直接就被覆盖掉了。

4. 确定遍历顺序

遍历顺序这块挺有意思的，还是看递推公式：dp[i][j]只和它正上方的元素和左上方的元素有关，所以不管是先遍历背包（横向遍历，先遍历行），还是先遍历物品（纵向遍历，先遍历列），都能获得有效的正上方元素和左上方元素。所以使用二维dp数组怎么遍历都行。

5. 打印dp数组

1
2
3

0 15 15 15 15 
0 15 15 20 35 
0 15 15 20 35

01背包问题完整Java代码（二维dp数组）：

public static void main(String[] args) {
    int[] weight = {1, 3, 4};
    int[] value = {15, 20, 30};
    int bagsize = 4;
    testweightbagproblem(weight, value, bagsize);
}

public static void testweightbagproblem(int[] weight, int[] value, int bagsize) {
    int m = weight.length, n = bagsize+1;
    // dp[i][j]是容量为j的背包所能容纳[0, i]中任取物品所能获得的最大价值
    int[][] dp = new int[m][n];
    // 只初始化第0行，第0列不需要初始化，因为容量0的背包最大价值全是0
    for (int j = weight[0]; j < n; j++) {
        dp[0][j] = value[0];
    }
    // 从[1, 1]开始遍历
    for (int i = 1; i < m; i++) {
        for (int j = 1; j < n; j++) {
            if(j < weight[i])   // 容量j < 当前物品的重量，即当前物品无法放进背包
                dp[i][j] = dp[i-1][j];
            else                // 当前物品可以放进背包
                dp[i][j] = Math.max(dp[i-1][j], dp[i-1][j-weight[i]]+value[i]);
        }
    }
    //打印dp数组
    for (int i = 0; i < m; i++){
        for (int j = 0; j < n; j++){
            System.out.print(dp[i][j] + " ");
        }
        System.out.print("\n");
    }
}

一维dp数组（滚动数组）

还是动规五步曲：

1. 明确dp数组及下标含义

可以使用一维数组的原因是：发现在逐行遍历时，当前值只依赖于正上方和左上方，而只要把上一层的值拷贝到当前层，表达式完全可以是：
dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);。

dp[j]的含义是：容量为j的背包，背包物品的最大价值为dp[j]

2. 递推公式推导

递推公式可由dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);推导出：

dp[j] = max(dp[j], dp[j-weight[i]] + value[i])

3. dp数组初始化

关于初始化，一定要和dp数组的定义吻合，否则到递推公式的时候就会越来越乱。

dp[j]表示：容量为j的背包，所背的物品价值可以最大为dp[j]，那么dp[0]就应该是0，因为背包容量为0所背的物品的最大价值就是0。

也可以想象一下，本来是一个二维矩阵压缩成了一维；原本需要初始化第0列，现在就只需要初始化第0个元素；

但原本也初始化第0行了呀？那现在是不是整个一维数组也像二维数组的第0行一样进行初始化呢？

这样也不是不行，但是卡哥说了，现在是一维数组，dp[j]表示：容量为j的背包，所背的物品价值可以最大为dp[j]，像原来的第0行那样初始化肯定就不合适了。

4. 确定遍历顺序

遍历顺序这里还是有点讲究的。

for(int i = 0; i < weight.size(); i++) { // 遍历物品
    for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
    }
}

这里大家发现和二维dp的写法中，遍历背包的顺序是不一样的！

二维dp遍历的时候，背包容量是从小到大，而一维dp遍历的时候，背包是从大到小。

为什么呢？

倒序遍历是为了保证物品i只被放入一次！。但如果一旦正序遍历了，那么物品0就会被重复加入多次！

5. 打印dp数组

1
2
3

第0次遍历，dp数组的内容为：0,15,15,15,15,
第1次遍历，dp数组的内容为：0,15,15,20,35,
第2次遍历，dp数组的内容为：0,15,15,20,35,

01背包问题完整Java代码（滚动数组）：

public static void main(String[] args) {
    int[] weight = {1, 3, 4};
    int[] value = {15, 20, 30};
    int bagsize = 4;
    testweightbagproblem(weight, value, bagsize);
}

private static void testweightbagproblem(int[] weight, int[] value, int bagsize) {
    int m = weight.length, n = bagsize+1;
    // dp[j] 是容量j的背包，容纳物品的最大价值
    int[] dp = new int[n];
    // 初始化
    dp[0] = 0;
    // 倒序遍历，还是先遍历物品，再遍历背包
    for(int i = 0; i < m; i++) { // 遍历物品
        for(int j = bagsize; j >= weight[i]; j--) { // 遍历背包容量
            dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
        }
        // 循环打印dp数组的内容，观察数组的滚动
        System.out.print("第"+i+"次遍历，dp数组的内容为：");
        for (int e : dp) System.out.printf(e + ",");
        System.out.println();
    }
}