上次能获得视差图后,整个立体匹配算法的整体框架已经有了,剩下的就是优化工作了,优化肯定有个优先级,什么样的优化、怎样优化是需要我们自己根据实际的项目进行评估的,以优化匹配精度是需要牺牲一些效率的,我做的项目对精度的要求不是特别高,但需要做到实时,所以根据项目情况进行优化吧。
首先第一个做的优化是代价聚合,这应该都不叫优化了,但我还是把他归为优化一类,因为从效果来看,上次的确是已经获得深度图了,根据Stereo Vision:Algorithms and Applications的ppt讲义可以知道,代价聚合也是半全局算法SGM绕不开的,所以就接着搞吧。
还是跟着李迎松博士的博客搞得,代价聚合使用SO(Scanline Optimizaion)算法,即扫描线优化算法。
视差主序
看过前篇的同学们肯定已经接触了视差主序的概念,我再次重申一遍是因为它很重要,关系到我如何存取代价数组的值。
我们谈到主序,大家会想起二维数组中数据的存储方式,如果是行主序,则数据优先在行内按顺序紧密排列,即第0行第0列和第0行第1列是相邻的元素;如果是列主序,则数据优先在列内按顺序紧密排列,即第0行第0列和第1行第0列是相邻的元素。主序类型,决定了通过行列号计算元素在数组中相对首地址的位置偏移量的方式,也决定了数组采用哪种遍历顺序会更高效(缓存原理)。
代价数组有三个维度:行、列、视差,视差主序的意思是同一个像素点各视差下的代价值紧密排列,即代价数组元素的排列顺序为:
(0,0)像素的所有视差对应的代价值;
(0,1)像素的所有视差对应的代价值;
…
…
(0,w-1)像素的所有视差对应的代价值;
(1,0)像素的所有视差对应的代价值;
(1,1)像素的所有视差对应的代价值;
…
…
第(h-1,w-1)个像素的所有视差对应的代价值;这样排列的好处是:单个像素的代价值都挨在一起,聚合时可以达到很高的存取效率。这对于大尺寸影像来说可带来明显的效率优势,对于像CUDA这类存储效率至关重要的平台来说就有明显优势。
视差主序下,( i , j , d ) ( i, j, d )(i,j,d)位置的代价值由如下方式获得(cost为代价数组):
cost[i width disp_range + j*disp_range + d]
1
大家思考下为何是这样获取,理解下视差主序的含义。介绍完主序方式,就可以开始摄入正餐了!
一开始没太注重这个视差主序,后来在研究了一段时间李博的代码后才知道李博在文章最前面就将这个概念说明的用意,这是我的一点疑惑,并有幸得到了李博的解答:
问:SGM算法中的代价数组为什么使用一维数组而不使用多维数组呢,难道一维数组性能更好吗?
答:其实一般情况下使用都差不多,多维数组就是你用着方便。一维数组因为是连续的,所以会有缓存命中率高、可以任意转换指针类型(这个在CUDA的三维数组里会频繁使用)等优点,实际上如果你直接让编译器分配一个三维数组,他大概率就是底层分配的一维数组,再做一个偏移量管理。而如果你手动分配多个2维数组组合成3维数组,比如一个vector里面很多mat,那多个2维数组不是连续的,效率是会比连续的一维数组要慢一点。一维数组主要是要你自己计算偏移量,实际上使用更灵活,整体效率更好的。
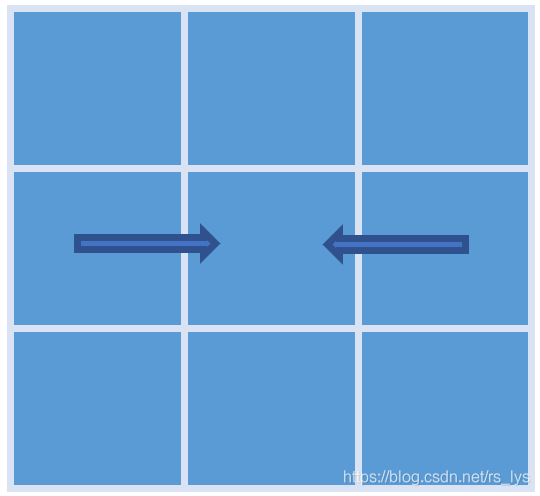
左右路径聚合
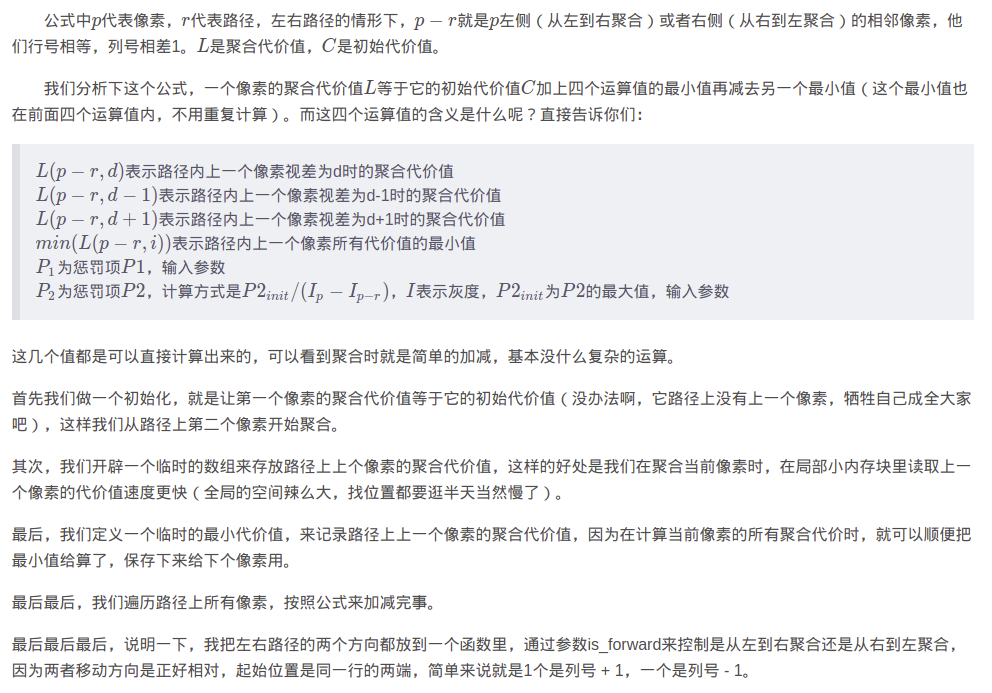
代价计算公式:
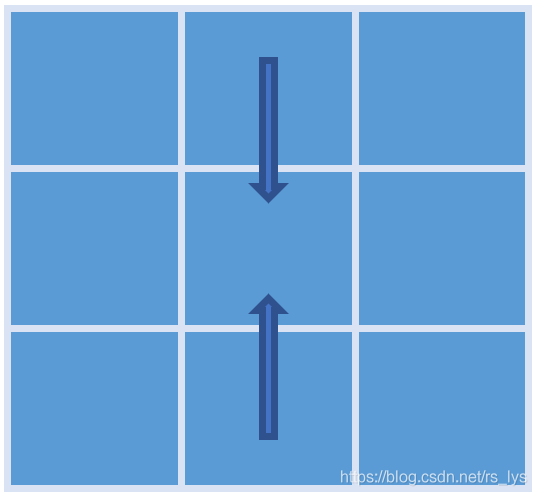
上下路径聚合
原理与左右路径聚合一致
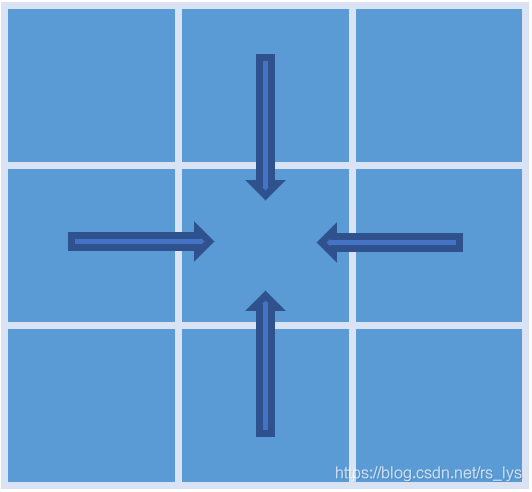
总路径聚合
四路径聚合已经能达到我的要求了,而且四路径比八路径效率更高,八路径会有不干活的情况。八路径聚合可看李博的这篇博客:代价聚合2
实验结果可看李博的博客。
1. 【码上实战】【立体匹配系列】经典SGM:(3)代价聚合 ↩