Census变换

发表于 | 分类于
字数统计: 1.4k | 阅读时长 ≈ 5

Census变换 2是什么

是一种非参数局部变换方法，通过变换两幅图像，使用相关性，以计算图像的匹配关系。依赖像素强度的相对顺序而不是强度值本身，所以对图像亮度不敏感。census变换是对局部空间结构的非参数化总结。

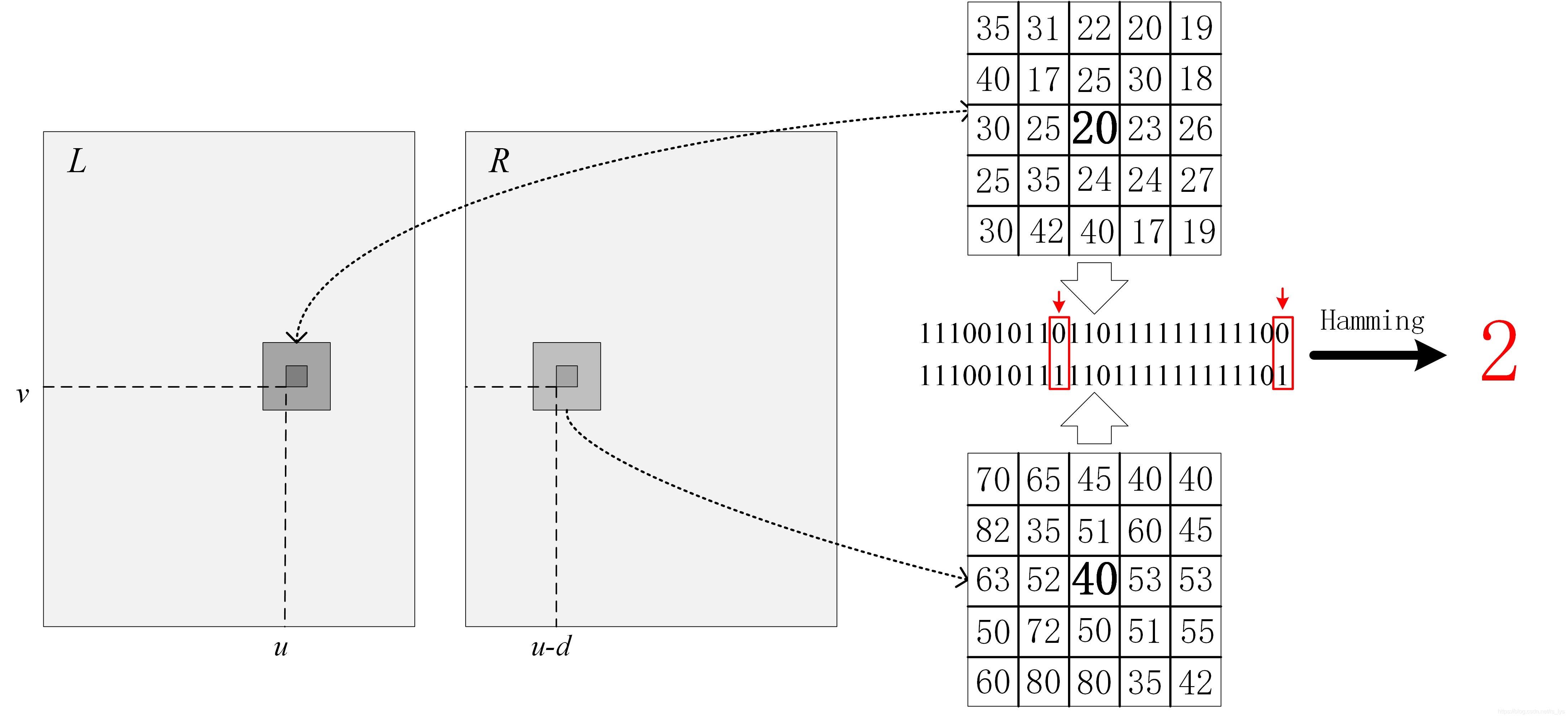
设$P$是一个像素，$I(P)$是像素强度（通常是一个8bit整数），$N(P)$是围绕$P$的直径为$d$的正方形邻域中的一组像素。所有非参数变换都取决于$P$与邻域$N(P)$中像素强度的比较结果：

非参数局部变换仅依赖于有序对集：

$R_{\tau}(P)$将像素P周围的局部邻域映射到表示强度小于$P$的相邻像素集的位串。设$N(P)=P \bigoplus D$，其中$\bigoplus$是Minkowski和，D是一组位移，设$\bigotimes $表示缩并（上标和下标相同的参数在相乘求和后，可看作标量）。则可以指定census变换：

利用Hamming距离（即两个位串中不同位的数目）来比较census变换后图像的两个像素的相似度。为了计算匹配关系，在应用census变换后最小化Hamming距离。

Hamming距离即两个比特串的对应位不相同的数量，计算方法为将两个比特串进行亦或运算，再统计亦或运算结果的比特位中不为1的个数：

gsUhcR.jpg

Census变换对整体的明暗变化并不敏感，因为是比较的相对灰度关系，所以即使左右影像亮度不一致，也能得到较好的匹配效果。

Census相比互信息还具有并行度高的优点，因为Census变换值是局部窗口运算，所以每个像素可以独立运算，这个特性让其可以很好的设计多线程并行计算模型，无论是CPU并行还是GPU并行都能达到非常高的并行效率。

大白话理解census变换与Hamming距离

census变换就是对一个像素的编码方式，使用这个像素周围的像素与其作比较，比它大就得1，否则就得0，所以就能得到一个二进制位串，这就完成了对这个像素的编码，这不是随意的，而是依赖他周围的像素，因为是互相比较得出的值，所以只能得出相对的信息，而忽略一些绝对的信息。

Hamming距离就是对两个二进制位串按位比较不同位的个数。

为什么

为了计算图像的匹配关系

怎么做

直接上代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
#include <iostream>
#include <opencv2/opencv.hpp>
#include <bitset>

using namespace std;
using namespace cv;

void census_transform_3x3(const uint8_t *source, uint32_t *census, const int32_t &width,
                          const int32_t &height){
    for (int32_t i = 1; i < height - 1; i++) {
        for (int32_t j = 1; j < width - 1; j++) {
            // 中心像素值
            const uint8_t gray_center = source[i * width + j];

            // 遍历大小为3x3的窗口内邻域像素，逐一比较像素值与中心像素值的的大小，计算census值
            uint32_t census_val = 0u;
            for (int32_t r = -1; r <= 1; r++) {
                for (int32_t c = -1; c <= 1; c++) {
                    census_val <<= 1;
                    const uint8_t gray = source[(i + r) * width +j + c];
                    if (gray < gray_center)
                        census_val += 1;
                }
            }
//            printf("%d", gray_center);
            // 中心像素的census值，为之后的代价计算做准备
            census[i * width + j] = census_val;
            // 打印二进制数
            cout<<"中心像素的二进制位串："<<bitset<9>(census_val)<<endl;
            // 打印十六进制数
//            printf("中心像素的十六进制位串：%x\n", census_val);
        }
    }
}

uint8_t Hamming32(const uint32_t &x, const uint32_t &y) {
    uint32_t dist = 0, val = x ^ y;

    // Count the number of set bits
    while (val){
        ++dist;
        val &= val - 1;
    }
    return dist;
}
int main() {
    Mat uM1 = Mat(3,3,CV_8UC1);	// 声明一个3x3的单通道矩阵
    Mat uM2 = Mat(3,3,CV_8UC1);	// 声明一个3x3的单通道矩阵
    randu(uM1,Scalar::all(0), Scalar::all(255));	// 对uM进行初始化，初始化值的范围为0～255
    randu(uM2,Scalar::all(0), Scalar::all(255));	// 对uM进行初始化，初始化值的范围为0～255
    cout << uM1 << endl;
    cout << uM2 << endl;

    int32_t width = uM1.cols;
    int32_t height = uM1.rows;
    auto *census1 = new uint32_t [width * height](); // 声明一个动态数组
    auto *census2 = new uint32_t [width * height](); // 声明一个动态数组
    // 窗口大小为3x3的 census 变换
    census_transform_3x3(uM1.data, census1, width, height);
    census_transform_3x3(uM2.data, census2, width, height);

    int Hamming = Hamming32(census1[4],census2[4]);
    cout << "Hamming:" << Hamming << endl;

    return 0;
}

结果验证：

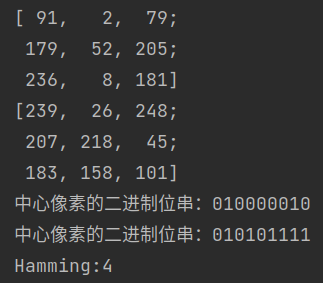
gsUufH.png

PS:

这里插一嘴，census变换的论文中，二进制位串的求法和代码 1里正好是相反的，但不会影响Hamming距离的结果，因为我理解census变换只是一种将图像信息转化为二进制的编码方式，只要两张图片都遵守这种编码方式就行，真正核心的地方就是Hamming距离来匹配图像了

1. 【理论恒叨】【立体匹配系列】经典SGM：（2）匹配代价计算之Census变换 ↩
2. ZABIH R, WOODFILL J. Non-parametric local transforms for computing visual correspondence[M]. 1994: 151-158. ↩