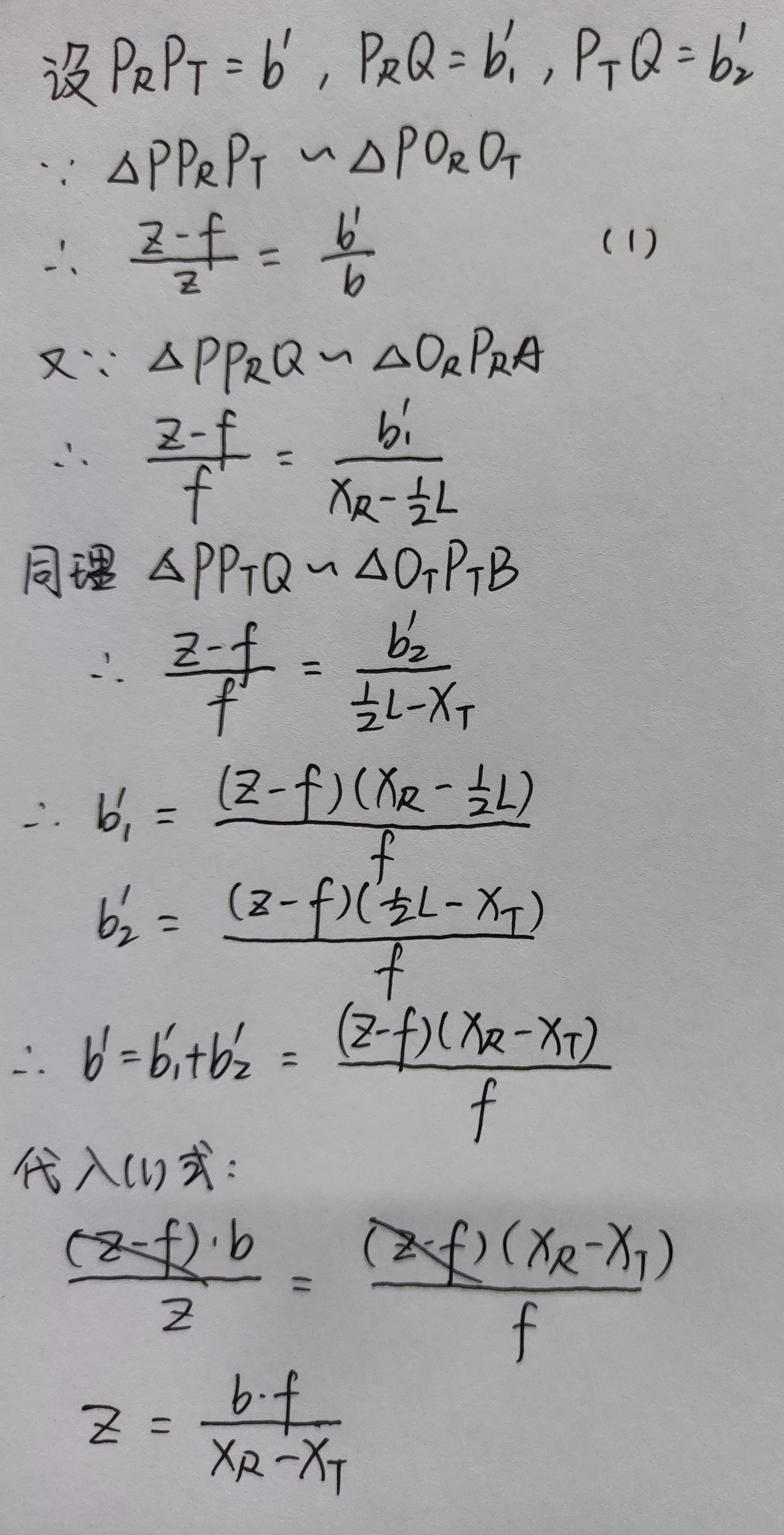对极几何

发表于 | 分类于
字数统计: 1.4k | 阅读时长 ≈ 5

双目视觉的对极几何

  1. 对极几何是什么？

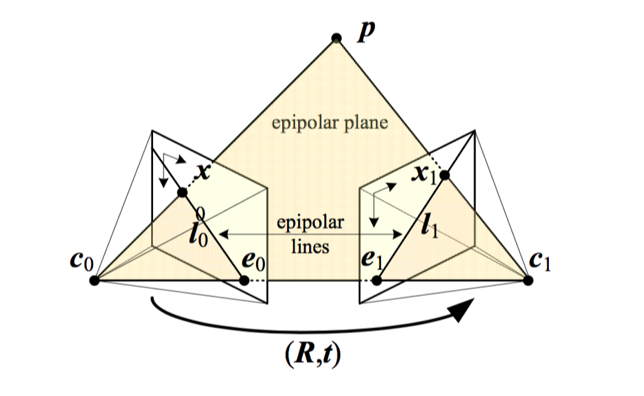
    对极几何是相机在两个不同的位置生成的两幅图像，其拍摄位置和生成图像之间存在特殊的几何关系。其基本几何模型如下：

    gYkU6s.png

  2. 对极几何的作用

    1. 解决立体匹配的问题，这里把C0和C1想象成两个相机，各获得一副图像，图像的内容会存在一定的约束关系，依靠这种关系，我们可以确定物体的深度
    2. 解决相机位姿与拍摄点的相对位置问题。把C0和C1想象成一个相机在两个不同的位置获得的两幅图像，根据约束关系，可以推导出相机的位姿。

    双目主要利用第一条。

  3. 基本概念

    1. 极点（Epipoles）：两个相机得基线与两个成像平面得交点，如上图中的e0、e1
    2. 极线（Epipolar Lines）：空间中点在成像平面上的投影点与极点的连线，如上图中的l0、l1
    3. 极平面（Epipolar Plane）：空间中的点与两个相机的光轴中心点所组成的平面，如上图c0、c1、p所在的平面

  4. 对极约束

    假定相机参数已知，那么对于空间中P点，它将和两个相机的中心点O1和O2，唯一确定对极几何的几何关系，极点、极线、极平面都将确定，而对极约束描叙的就是：在平面1上成像为p的所有空间点，其必定投影在平面2的极线上，反之亦然。

双目相机获得深度图的原理

双目相机获得深度图的原理

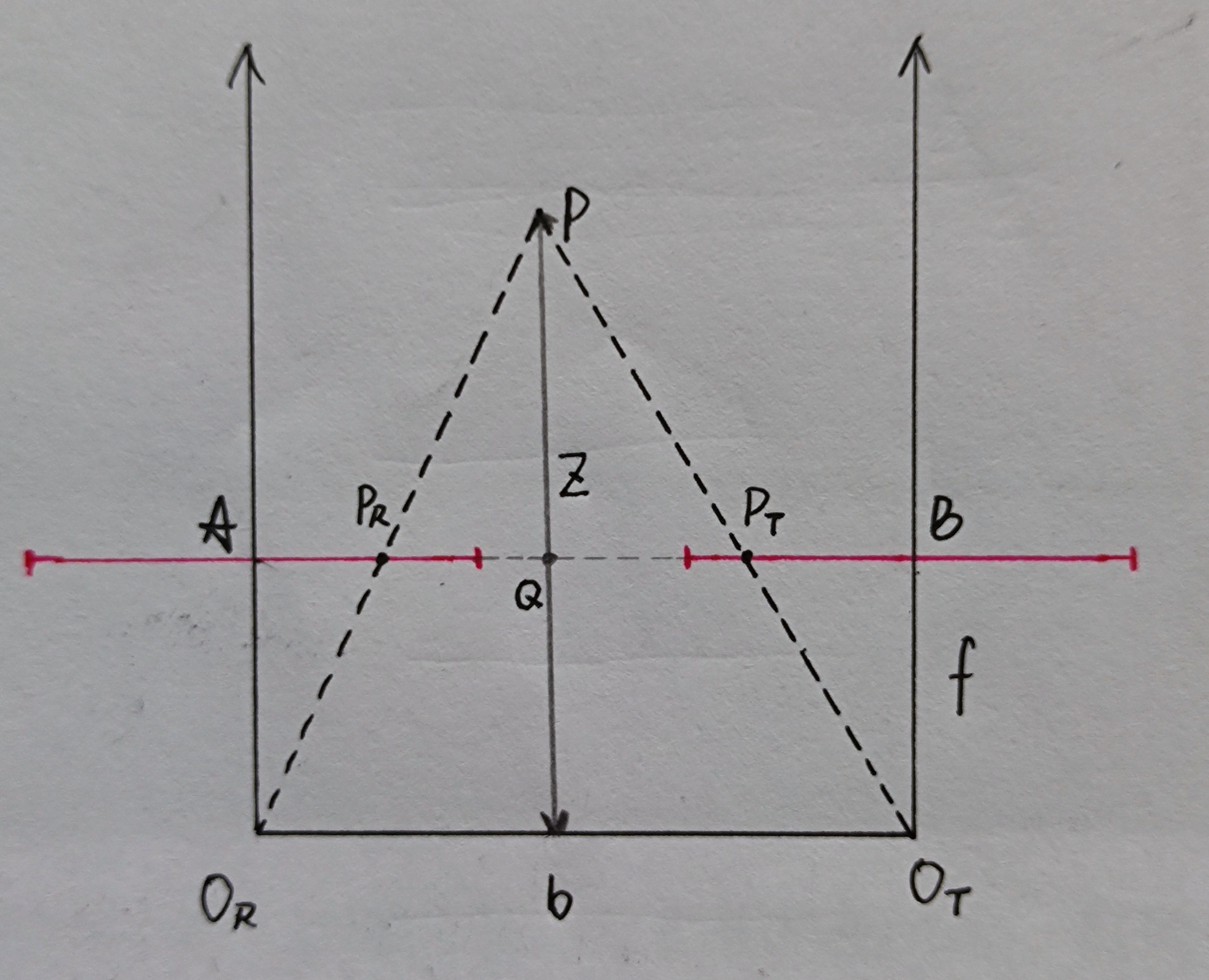
guK3WR.jpg

如图，可抽象为双目相机成像的鸟瞰图，$O_{R}$与$O_{T}$分别为左右相机的光心，红色线为相机CCD，$A$、$B$为相机CCD的中点，设相机CCD的长度为$L$，物体P在左右相机的CCD上的像点分别为$P_{R}$、$P_{T}$，像点距离CCD左端的距离分别为$x_{R}$、$x_{T}$，相机的焦距为$f$，相机光心的距离为$b$，求物体的距离$Z$

gul3Wj.jpg

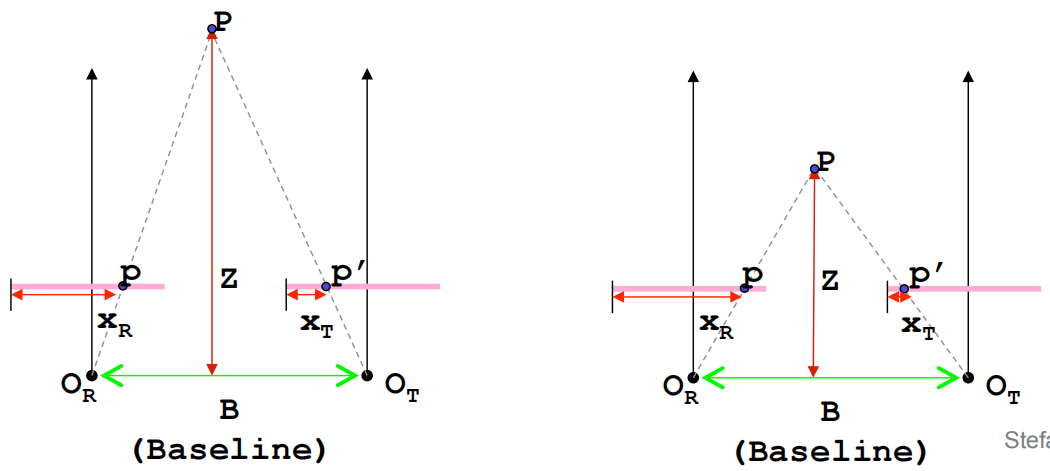
视差：

gul4te.png

物体越近，视差越大；物体越远，视差越小。

关键矩阵

双目相机获得的图像存在约束关系，这种约束关系就是靠这三个关键矩阵来描述的：本质矩阵、基础矩阵、单应性矩阵。它们可以建立两个视图公共点之间的坐标联系，或者完成公共点之间的坐标转换。它们就像立体视觉双视图之间的桥梁，让彼此紧密相连，形成一个整体，才算有了立体视觉系统的概念。

本质矩阵和基础矩阵

变量说明：

  1. d1、d2为深度，是一个标量
  2. K1、K2为左右相机的内参
  3. R、t为旋转和平移矩阵
  4. p1、p2为图像坐标系
  5. x1、x2为像素坐标系

设空间点p在左相机坐标系下的坐标为P，则在右相机坐标系下的坐标为RP+t；在左右像平面上的投影为p1和p2，则：

等号左边的p齐次坐标，如果对空间点也取齐次，即将空间点归一化到$Z=1$的平面，d就变成了1，上式变成：

将矩阵K移到等号左边：

设：

则：

两边左叉乘 t ：

其中，

所以：

两边左乘$x_{2}^{\mathrm{T}}$：

左边显然等于0，则：

其中的$t\times R$就成为本质矩阵，用E表示：

也可以记为：

其中$t\verb!^!$为t的反对称矩阵。

将(1)式代入(2)式中，可得：

即：

其中的$K_{2}^{\mathrm{-T}}t\verb!^!RK_{1}^{-1}$称为基础矩阵，用F表示：

单应性矩阵

直接将左视图像素坐标转换到右视图像素坐标。特定条件是同一平面。表达式：

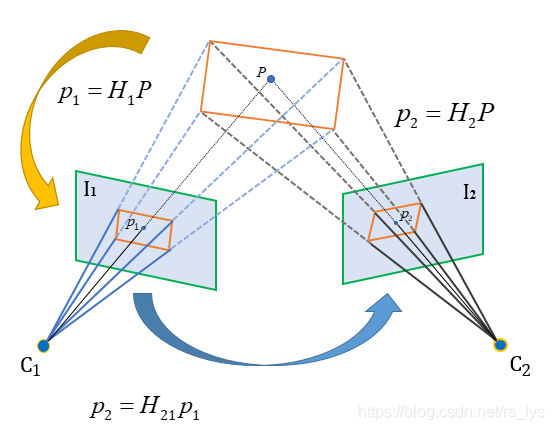
单应性矩阵不仅可以描述同一平面的像素点之间的关系，而且同一个平面在任意坐标系之间都可以建立单应性变换关系。比如影像坐标系与影像坐标系之间，世界坐标系和影像坐标系之间，如下图所示：

gYdxhT.png

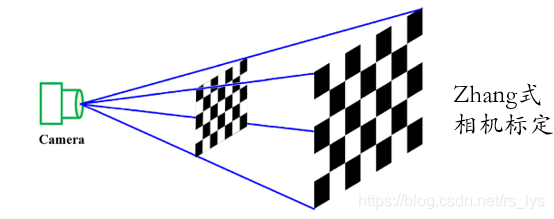
在双目立体视觉内，单应性变换是张式相机标定法的理论基础，纯平的标定板平面和影像平面存在单应性变换关系，同时它们存在世界坐标系到影像坐标系之间的投影变换关系，两个关系对等即可解出相机的内外参数。

gYwVN6.png

参考

立体视觉入门指南（2）：关键矩阵（本质矩阵，基础矩阵，单应矩阵）

对极几何的理解

(3)式中

是为什么呢？

  1. t叉乘x2的结果向量必定垂直于x2
  2. x2的转置必定与这个结果向量垂直
  3. 所以结果为0