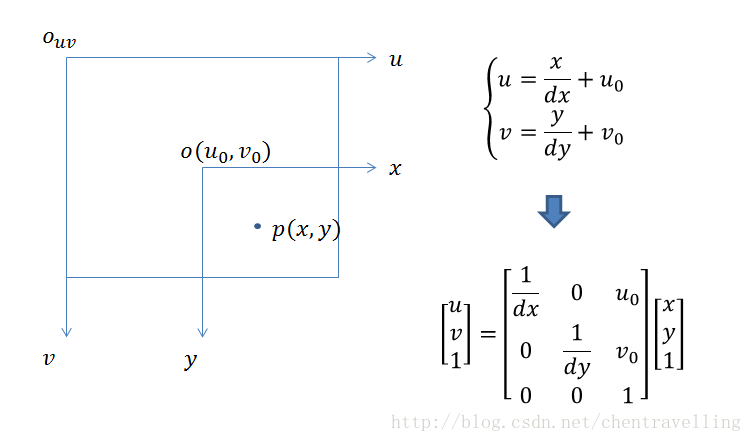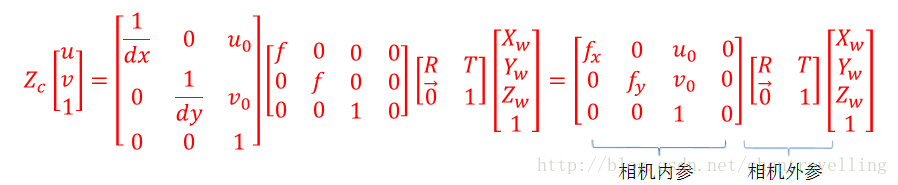相机的标定与矫正

在讲解什么是标定与矫正前，有必要梳理一下相机的成像原理。

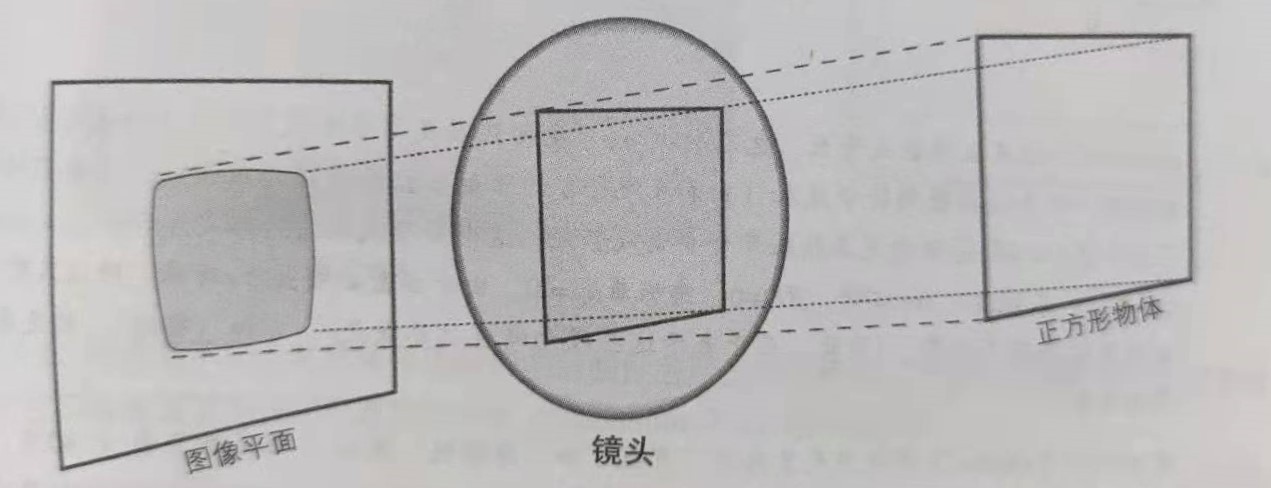
相机是一个比较复杂的光学系统，但可以将其抽象为一个理想的几何模型：小孔成像

成像原理

光线经过一个光学系统，在成像元件上可以获得像。

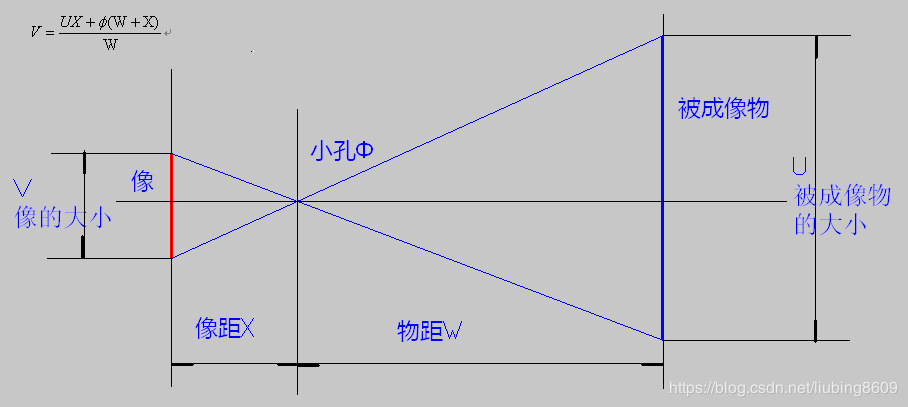
小孔成像

$$\frac{U}{V}=\frac{W}{X}$$

因为小孔成像不能为CCD成像提供足够的光线，所以引入了透镜，从而汇集更多的光线，但这也带来了畸变

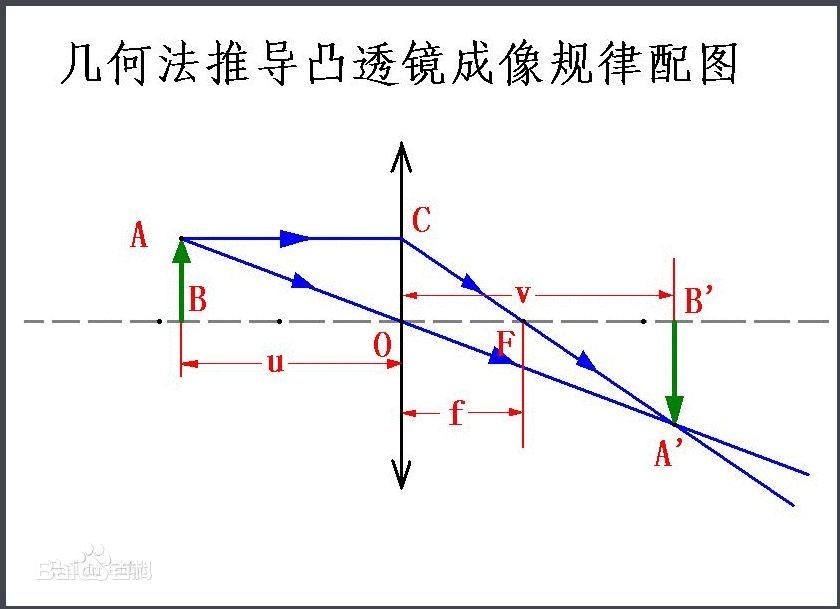
理想透镜成像¹

$$\frac{1}{f}=\frac{1}{u}+\frac{1}{v}$$

相机成像过程

基于理想光学透镜的成像原理，再辅以四种坐标系的变换，现实世界中的物体就可以映射为图像了

四大坐标系

1. 世界坐标系：描述世界中物体位置的绝对坐标系
2. 相机坐标系：以相机为原点建立的坐标系，单位为m
3. 图像坐标系：光心对应图像上的点，以其为原点建立的坐标系
4. 像素坐标系：图像的左上角为原点建立的坐标系

坐标系间的变换

为了方便计算，引入了齐次坐标

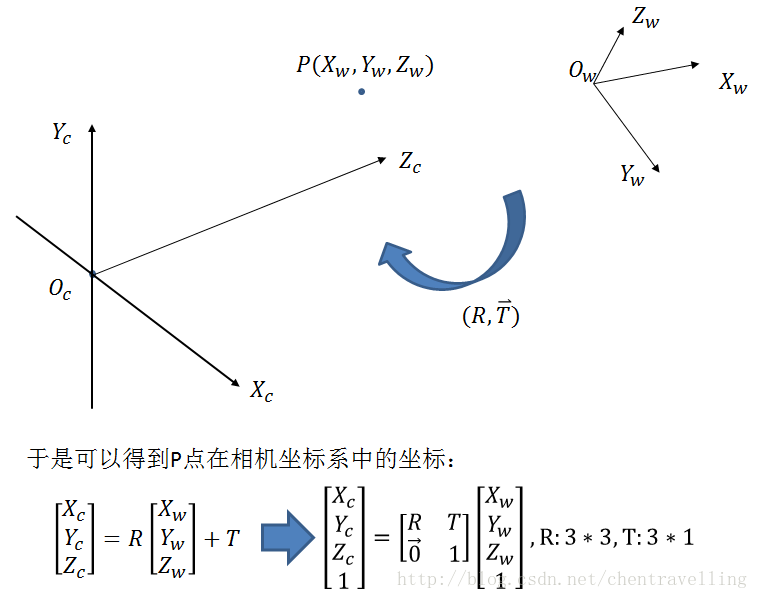
世界坐标系→相机坐标系

转换矩阵为：

$$\begin{bmatrix} R & T\\ \vec{0} & 1 \end{bmatrix}$$

R为旋转矩阵，T为平移矩阵

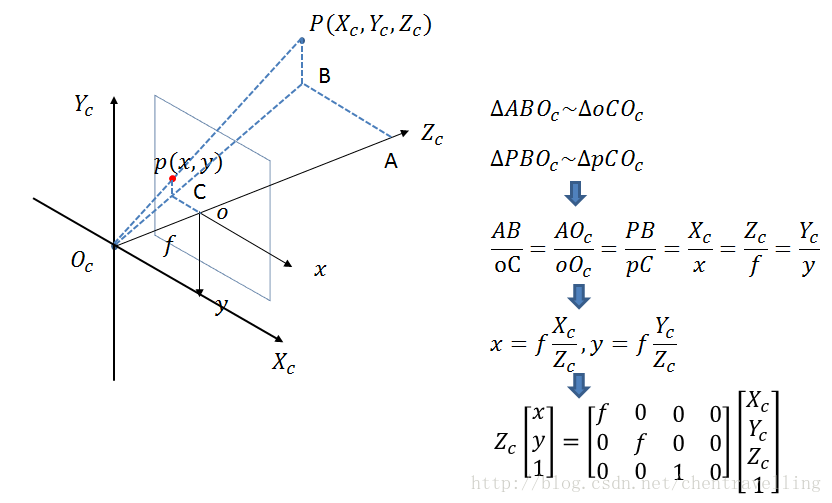
相机坐标系→图像坐标系

投影透视关系，从3D转换到2D，在这一过程中，深度信息丢失，怎么丢失的呢？

在投影透视关系中，物理世界中的一点在直线pP上时，都会被投影到图像上的同一点，二维的直线被压缩成了一维的点，在这个过程中，丢失了一个维度的信息。

观察这个计算：

$$Z_{C}\left[\begin{array}{l} x \\ y \\ 1 \end{array}\right]=\left[\begin{array}{llll} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & 1 & 0 \end{array}\right]\left[\begin{array}{c} X_{c} \\ Y_{c} \\ Z_{c} \\ 1 \end{array}\right]$$

等号左边有一个公有系数Zc，移到等号右边，变为：

$$\left[\begin{array}{l} x \\ y \\ 1 \end{array}\right]=\left[\begin{array}{llll} \frac{f}{Z_{C}} & 0 & 0 & 0 \\ 0 & \frac{f}{Z_{C}} & 0 & 0 \\ 0 & 0 & \frac{1}{Z_{C}} & 0 \end{array}\right]\left[\begin{array}{c} X_{c} \\ Y_{c} \\ Z_{c} \\ 1 \end{array}\right]$$

此时投影点p的单位还是mm，并不是pixel，需要进一步转换到像素坐标系。

图像坐标系→像素坐标系

dx与dy分别表示每个像素在横轴x和纵轴y上的物理尺寸，单位为:毫米/像素。那么x/dx的单位就是像素了。即最后u与v的单位变成了像素。转换矩阵为：

$$\left[\begin{array}{ccc} \frac{1}{d x} & 0 & u_{0} \\ 0 & \frac{1}{d y} & v_{0} \\ 0 & 0 & 1 \end{array}\right]$$

综上

通过上面四个坐标系的转换就可以得到一个点从世界坐标系如何转换到像素坐标系

即：

$$\left[\begin{array}{l} u \\ v \\ 1 \end{array}\right]=\frac{1}{Z_{C}} \times\left[\begin{array}{cccc} \frac{f}{d x} & 0 & u_{0} & 0 \\ 0 & \frac{f}{d x} & v_{0} & 0 \\ 0 & 0 & 1 & 0 \end{array}\right] \times\left[\begin{array}{cc} R & T \\ \overrightarrow{0} & 1 \end{array}\right] \times\left[\begin{array}{c} X_{W} \\ Y_{W} \\ Z_{W} \\ 1 \end{array}\right]$$

相机标定²

标定，主要是指使用标准的计量仪器对所使用仪器的准确度（精度）进行检测是否符合标准，一般大多用于精密度较高的仪器。标定也可以认为是校准。

所以我理解，相机标定是校准相机，方便我们进行后边的工作。具体一点，害！还是求内参。

相机的标定原理是比较复杂的，如果想探寻原理，非张正友标定法不看了，这里我只想追求结果，就先不看他了。

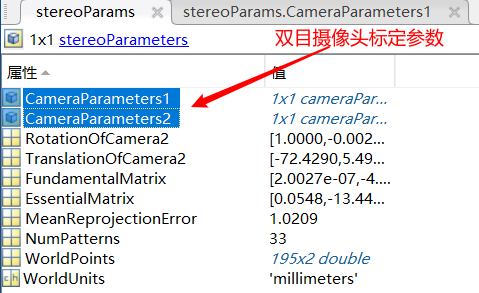
用Matlab进行双目相机标定

具体操作看这篇博客，这里只对结果进行简单的分析

主要看这些参数：

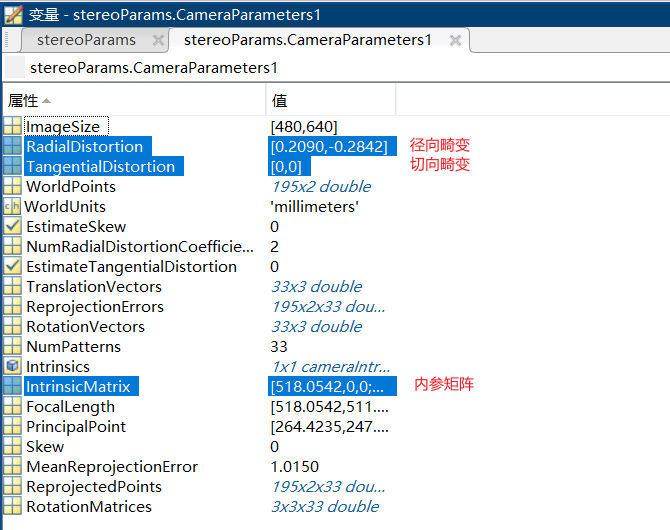
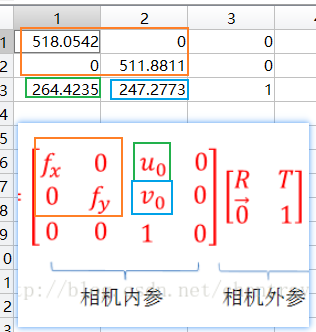
内参矩阵：

这里的f也不是真的焦距，而是f/dx和f/dy；Matlab求出的内参矩阵是转置过的，在程序中使用时还需要再转置回去。

分析一下标定结果：

1. 图片分辨率为640*480，u0 = 264, v0 = 247，

   u0,v0是图像中心点的坐标。而u0应该等于320，v0应该等于240，误差很大

2. “焦距”=518

畸变矫正

之前在引入理想透镜成像中，我们引入了畸变，现在该解决畸变问题了，详细可看这篇博客的畸变部分的讲解。

1. 径向畸变：由于透镜的形状造成。对于透镜来说，远离透镜中心的光线比靠近透镜中心的光线更加弯曲。
   eg：鱼眼畸变，桶形畸变
2. 切向畸变：相机的组装造成。制造缺陷，透镜与成像平面不平行。感光元件CCD不是矩形，而是平行四边形

解决畸变问题只需要在写程序时加载畸变参数就可以矫正图像了，Opencv也有相应的接口。

这里想注明一下参数

畸变参数的一般顺序是k1,k2,p1,p2,k3。之所以把k3放在最后其实也很容易理解，因为前面说了一般k1,k2用来处理径向畸变足矣，k3相对而言用的比较少。 在获得了畸变参数以后，也就找到了真实观测的带畸变的像素与无畸变的像素间的关系，重采样即可实现影像校正。

在这里径向畸变参数k1=0.2090, k2=-0.2842；切向畸变参数p1=0, p2=0。

¹. 来自百度百科成像公式 ↩

². 到底什么是标定 ↩