边缘检测
卷积运算“$*$”
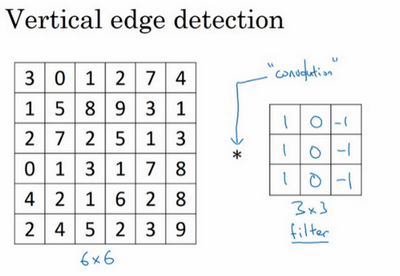
$*$是卷积的标准符号
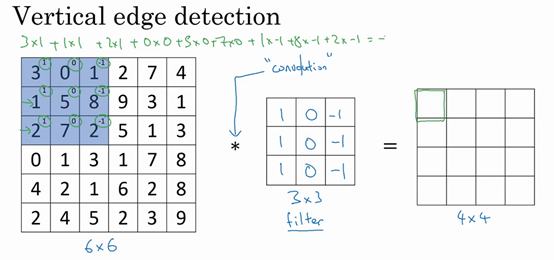
$3+1+2+0+0+0+(-1)+(-8)+(-2)=-5$即为卷积计算。
$n \times n$的图像用$f \times f$的过滤器卷积,得到$(n-f+1)\times(n-f+1)$的矩阵。
边缘检测
- 正边:边缘由亮到暗
- 复边:边缘由暗到亮
- 垂直边缘:
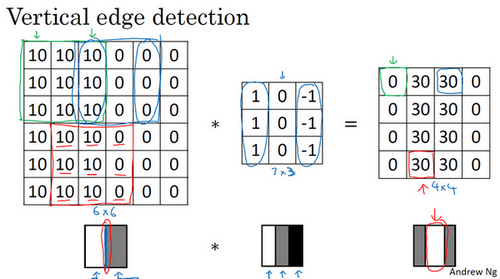
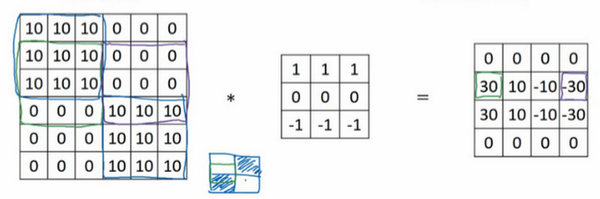
- 水平边缘:
滤波器:
- Sobel滤波器:
- Scharr滤波器:
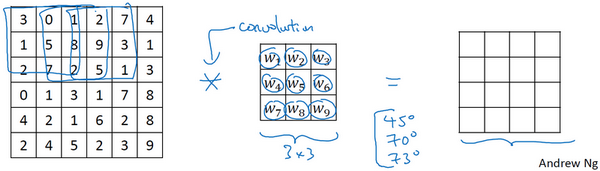
将矩阵中所有的数字视为参数,通过数据反馈,让神经网络自动去学习它们,我们会发现神经网络可以学习一些低级的特征,例如这些边缘的特征。相比这种单纯的垂直边缘和水平边缘,它可以检测出45°或70°或73°,甚至是任何角度的边缘。
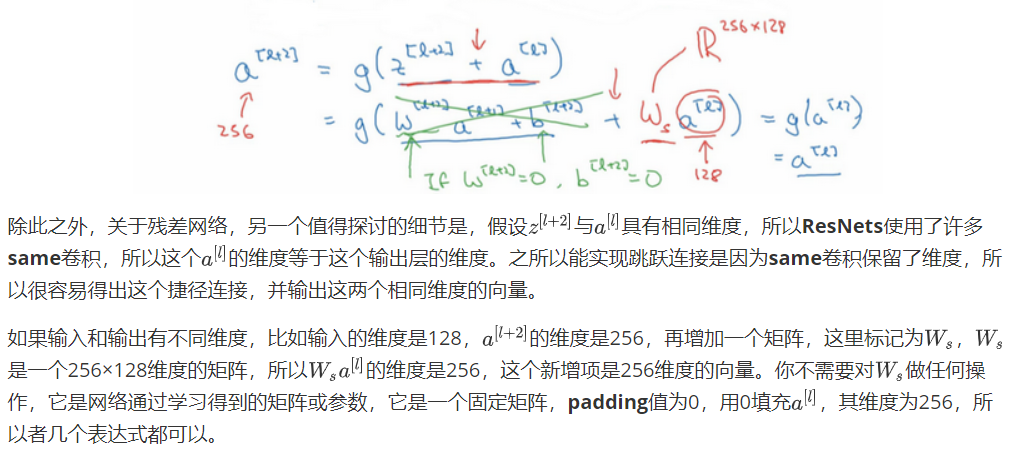
Padding
在图像的最外层用0进行数据填充。
为了解决以下两个问题:
- 越卷积,图像越小
- 图像边缘位置特征部分丢失:图像边缘的数据被采用的较少
两种填充方式:
Valid卷积:不填充
Same卷积:输入输出大小相同
$f$通常是奇数,原因:
- 如果是偶数,只能使用一些不对称填充。
- 使用奇数过滤器可以有一个中心点,方便指出过滤器的位置。
卷积步长
过滤器每次横向移动的距离
$n \times n$的图像用$f \times f$的过滤器卷积,步长为$S$,得到$\left \lfloor \frac{n+2p-f}{S}+1 \right \rfloor\times\left \lfloor \frac{n+2p-f}{S}+1 \right \rfloor$的矩阵。
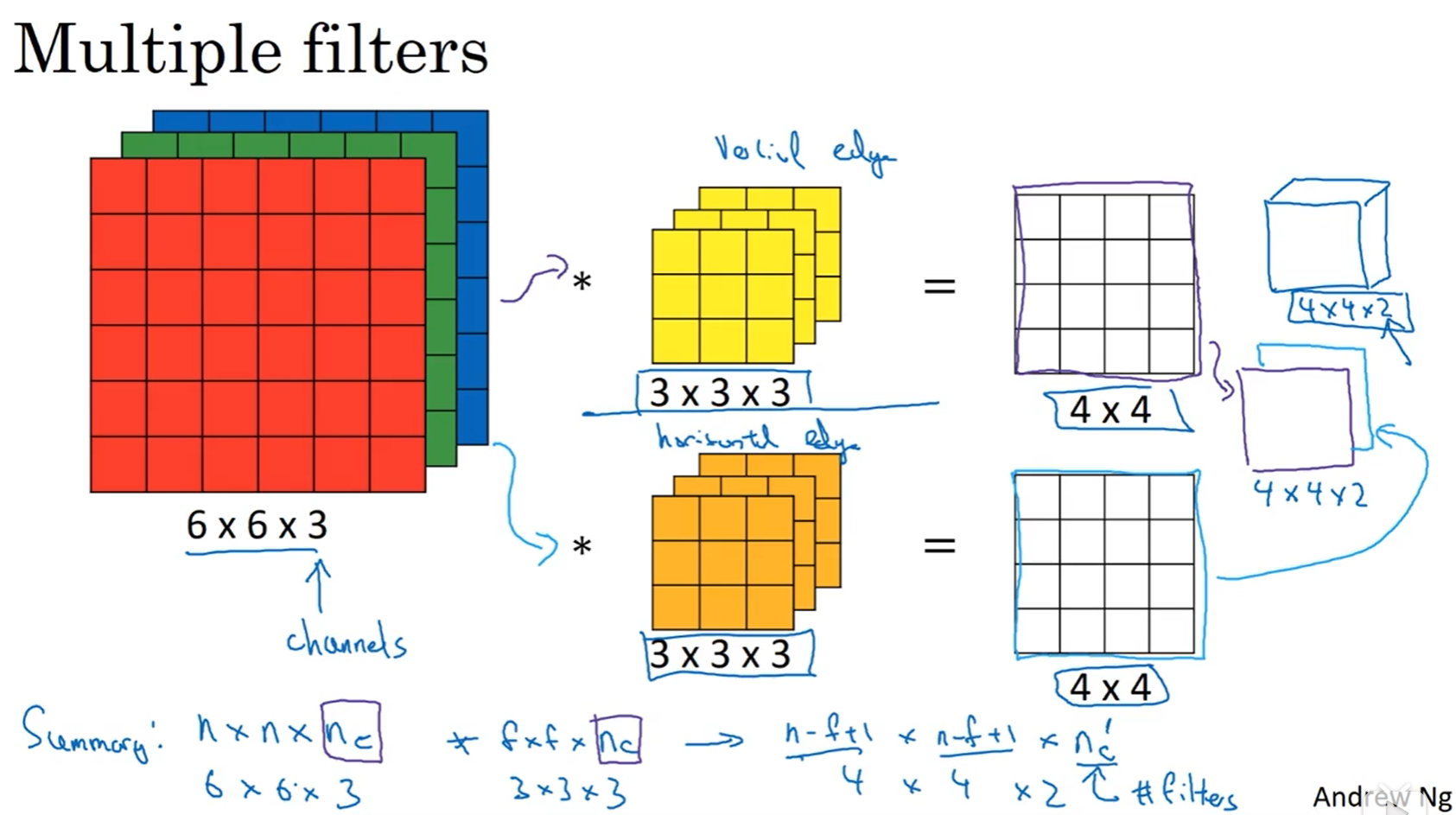
三维卷积
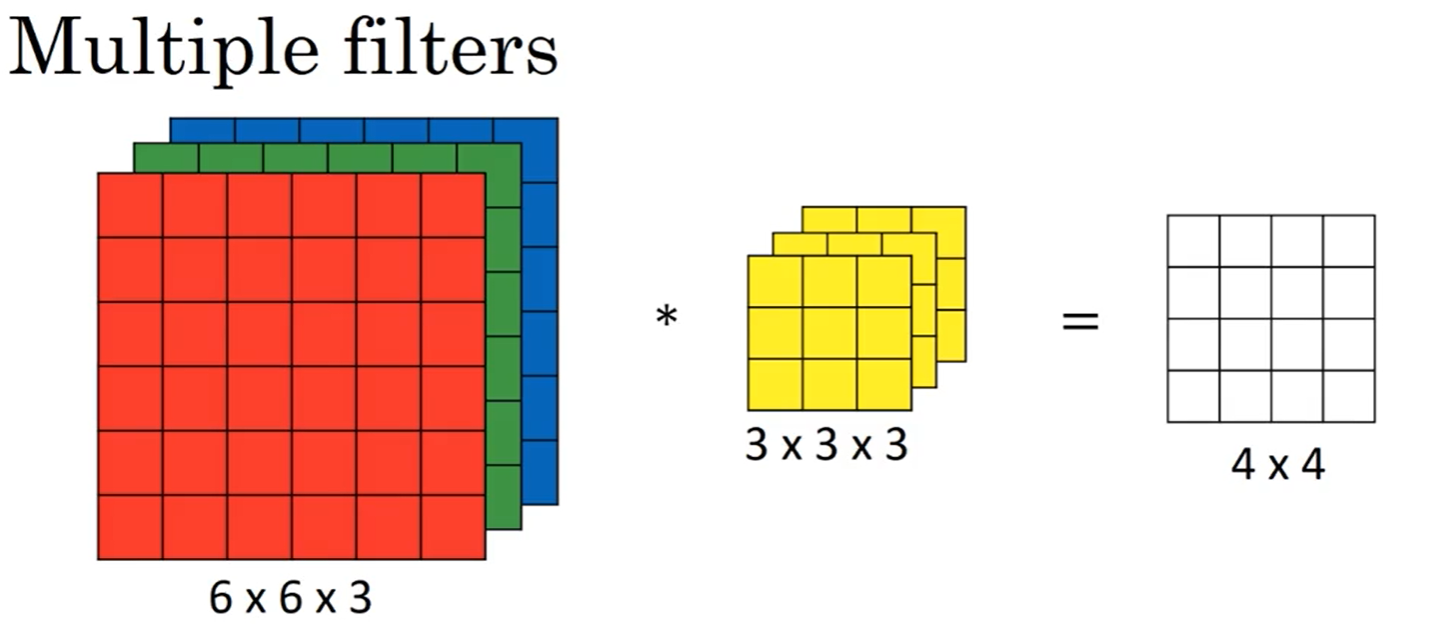
多种特征匹配卷积,使用n个不同的过滤器对矩阵进行卷积运算,然后将卷积后的一维矩阵叠加为新的n维矩阵:
池化层
缩减模型的大小,提高计算速度,同时提高所提取特征的鲁棒性
- MaxPooling
- AveragePooling
为什么使用卷积
卷积层的两个主要优势:参数共享和稀疏连接。使得神经网络的参数大大减少。
- 参数共享
共享的就是过滤器中的参数,这个过滤器可以匹配图片中的所有相同类型的特征,从而减少参数 - 稀疏连接
输出通过过滤器过滤输入特征,这些输出是彼此独立的,不会互相影响。
经典网络
- LeNet
- AlexNet
- VGG-16
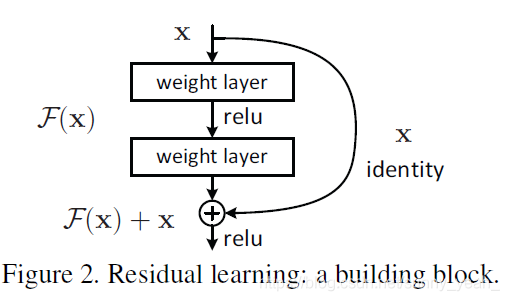
残差网络
ResNet(Residual Network)
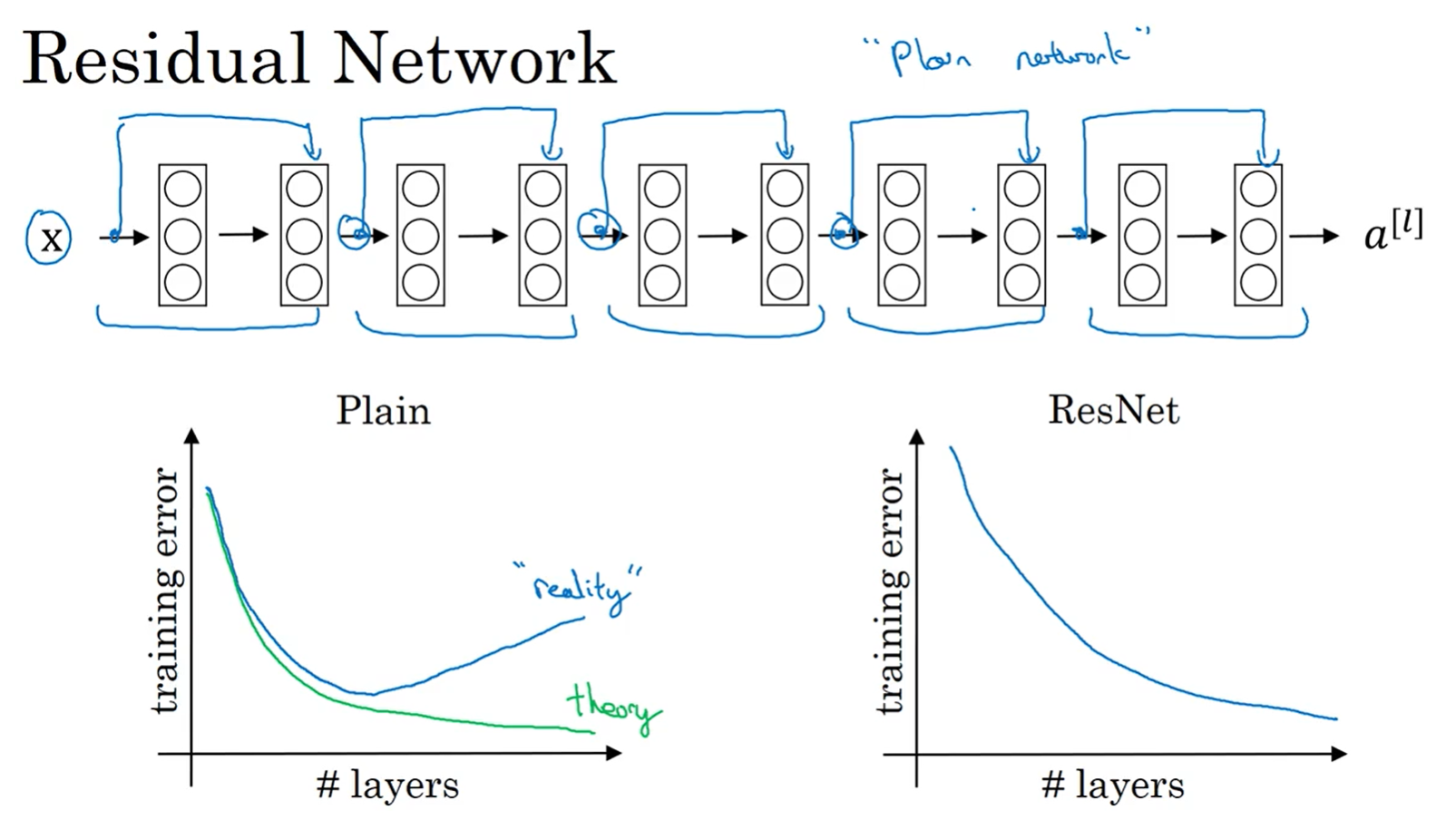
每两层增加一个捷径,构成一个残差块。如图所示,5个残差块连接在一起构成一个残差网络:
如果没有残差网络,对于一个普通网络来说,深度越深意味着用优化算法越难训练。实际上,随着网络深度的加深,训练错误会越来越多。
但有了ResNets就不一样了,即使网络再深,训练的表现却不错,比如说训练误差减少,就算是训练深达100层的网络也不例外。有人甚至在1000多层的神经网络中做过实验,尽管目前我还没有看到太多实际应用。但是对的激活,或者这些中间的激活能够到达网络的更深层。这种方式确实有助于解决梯度消失和梯度爆炸问题,让我们在训练更深网络的同时,又能保证良好的性能。也许从另外一个角度来看,随着网络越来深,网络连接会变得臃肿,但是ResNet确实在训练深度网络方面非常有效。
残差网络为什么有用
残差网络使用ReLU作为激活函数,残差块学习恒等函数非常容易,从而确定网络学习不受影响,甚至残差块能提高性能,至少不会降低性能。
1×1卷积
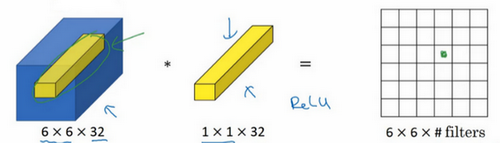
相当于6×6=36个单元格,对每一个单元格所在的信道做了一个全连接网络,所以1×1卷积又叫网络中的网络。
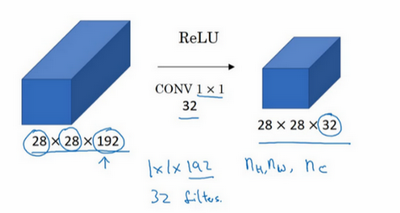
使用池化层可以压缩高度和宽度,使用1×1卷积可以控制信道数。
可以用32个大小为1×1的过滤器,严格来讲每个过滤器大小都是1×1×192维,因为过滤器中通道数量必须与输入层中通道的数量保持一致。但是你使用了32个过滤器,输出层为28×28×32,这就是压缩通道数的方法
Inception网络
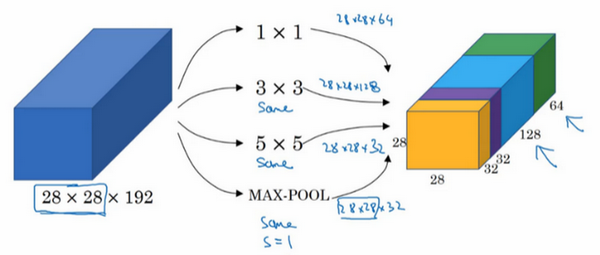
使用不同的卷积核对某个输入量进行卷积,并将结果叠加在一起组成新的输出,这样一个单元称为Inception网络的基本单元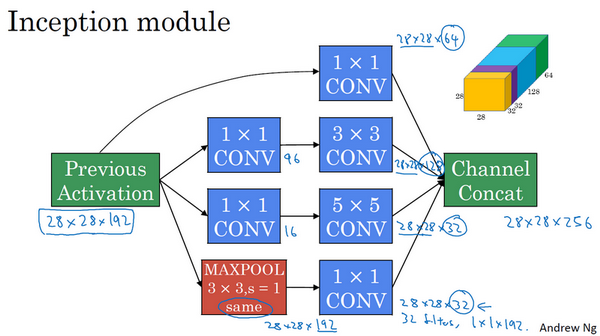
将这些基本模块组合起来就形成了Inception网络: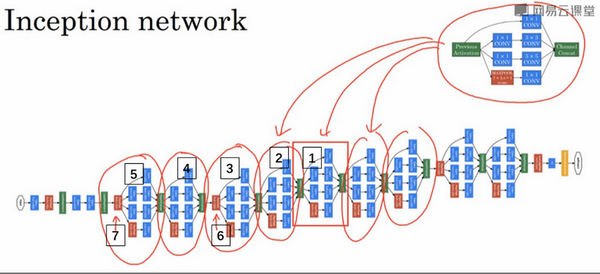
迁移学习
你拥有的数据越多,你需要冻结的层数越少,能够训练的层数就越多。
如果有大量数据,就可以把预训练的整个网络作为一个初始化,然后重新训练整个网络