这篇有点水,Batch Norm还是不太理解,很多笔记是直接摘抄的
调试处理
超参数优先级排序:
- 学习率$\alpha$
- Momentum算法中的$\beta$;隐藏层单元数量;mini-batch大小
- 神经网络层数;学习率下降参数;$\beta_{1}=0.9,\beta_{2}=0.999,\varepsilon=10^{-8}$
超参数搜索:
在参数空间中随机取值:
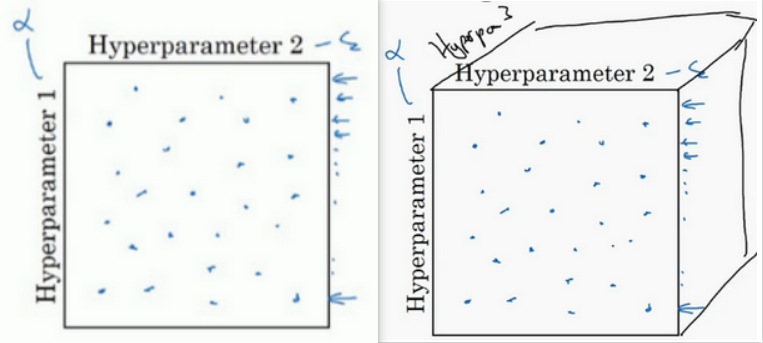
粗糙到精细的策略:
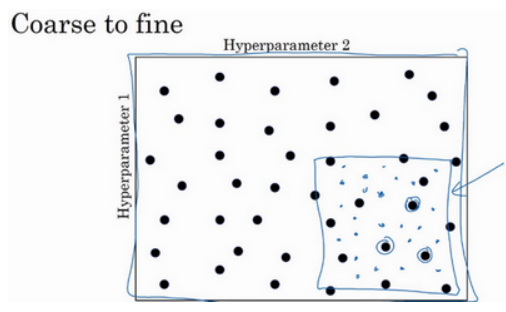
先在参数空间中随机选择,发现最优值大概在某一区域分布时,则放大这块小区域,在这块小区域中更密集地取值或随机取值。
为超参数选择合适的范围
放弃线性轴而选择对数轴搜索超参数。
因为在不同的区域,超参数微小的变化对模型的优化影响不同,这显然是不公平的。
例如:在[0.0001,1]这个范围内取值时,如果采用线性轴,在[0.0001,0.1]这个区域中的计算资源仅占10%,而在[0.1,1]这个区域中的计算资源占90%,这样不太好。而采用对数轴,分别依次取0.0001,0.001,0.01,0.1,1,在对数轴上均匀随机取点,这样,在0.0001到0.001之间,就会有更多的搜索资源可用。
在python中,对数轴取值这样做:
1 | r = -4 * np.random.rand() |
对于$\beta$,道理同上 :$\beta \in [0.9,0.999]$,我们只需要讨论$1-\beta$的范围,即$[0.1,0.001]$(这里颠倒了,是因为能够与[0.9,0.999]对应上)
为什么用线性轴取值不是个好办法,这是因为当$\beta$接近1时,所得结果的灵敏度会变化,即使有微小的变化。所以$\beta$在0.9到0.9005之间取值,无关紧要,你的结果几乎不会变化。但值如果在0.999到0.9995之间,这会对你的算法产生巨大影响。
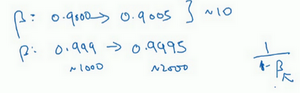
超参数调试实践
关于如何搜索超参数的问题,大概两种重要的思想流派或人们通常采用的两种重要但不同的方式:
- Babysitting one model
像个保姆一样,精心的照看一个模型,耐心地调整学习率以及各个超参数,以希望模型的损失越来越低,性能越来越好。 - Training Many models in parallel
同时训练很多模型,但是不怎么管,最后只挑那个表现最优秀的。
计算资源多,选第二种,否则没得选,安心当保姆
归一化网络的激活函数
吴恩达老师讲的归一化激活函数真正归一的对象是$z=wx+b$中的$z$
前三个公式将z值进行了归一化。
第四个公式会将正规化后的数据进行缩放和平移变换。$\gamma$和$\beta$是两个需要学习的参数,通过学习调整到合适的值。
这段笔记有助于理解归一化的意义:
Batch Norm为什么奏效
和输入归一化类似,使均值为0,方差为1,从而加速学习。
使权重比网络更滞后或更深层,相比于神经网络中前层的权重,后层更能经受得住变化。
Batch归一化减少了输入值改变的问题,它的确使这些值变得更稳定,神经网络的之后层就会有更坚实的基础。即使使输入分布改变了一些,它会改变得更少。它做的是当前层保持学习,当改变时,迫使后层适应的程度减小了,你可以这样想,它减弱了前层参数的作用与后层参数的作用之间的联系,它使得网络每层都可以自己学习,稍稍独立于其它层,这有助于加速整个网络的学习。
我会把Batch归一化当成一种正则化,这确实不是其目的,但有时它会对你的算法有额外的期望效应或非期望效应。但是不要把Batch归一化当作正则化,把它当作将你归一化隐藏单元激活值并加速学习的方式,我认为正则化几乎是一个意想不到的副作用。
测试时的Batch Norm
在训练时,$\mu$和$\sigma^{2}$是在整个mini-batch上计算出来的,但在测试时,你可能需要逐一处理样本,方法是根据你的训练集估算$\mu$和$\sigma^{2}$,估算的方式有很多种,理论上你可以在最终的网络中运行整个训练集来得到$\mu$和$\sigma^{2}$,但在实际操作中,我们通常运用指数加权平均来追踪$\mu$和$\sigma^{2}$的值。还可以用指数加权平均,有时也叫做流动平均来粗略估算$\mu$和$\sigma^{2}$,然后在测试中使用和的值来进行你所需要的隐藏单元值的调整。在实践中,不管你用什么方式估算$\mu$和$\sigma^{2}$,这套过程都是比较稳健的,因此我不太会担心你具体的操作方式,而且如果你使用的是某种深度学习框架,通常会有默认的估算$\mu$和$\sigma^{2}$的方式,应该一样会起到比较好的效果。但在实践中,任何合理的估算你的隐藏单元值的均值和方差的方式,在测试中应该都会有效。
Softmax回归
非逻辑回归,可以映射更多类别。一般在神经网络的最后一层。会将最后的结果归一化。
通常与交叉熵损失函数结合使用。