5.优化算法

Mini-batch梯度下降法

将较大的训练集分割为较小的子集，这些子集叫做mini-batch。

如果mini-batch的大小是2的n次方，代码运行的会快一点，64~512的mini-batch比较常见。

假设训练集有5000,000个样本，mini-batch的大小为1000，则整个训练集一共有5000个mini-batch；使用batch训练，遍历整个训练集，梯度下降法只能下降一次，使用mini-batch，遍历一次训练集可以下降5000次；mini-batch大小为1时，则为随机梯度下降，噪声会减小，但会失去所有向量化带来的加速，因为一次性只处理了一个训练样本，这样效率过于低下。选择适合的mini-batch大小。

1 epoch代表遍历一次训练集。

指数加权平均数

接下来我就翻译翻译，什么叫tmd的指数加权平均数。

1. 平均数：n个数据的总和除以n

   $$average = \frac{1}{n}\sum_{i=1}^{n}x_{i}$$

2. 加权平均数：每个数据乘以其权重，最后求和。

   $$average = \sum_{i=1}^{n}p_{i}x_{i},其中\sum_{i=1}^{n}p_{i}=1$$

3. 指数加权平均数：权值以指数形式存在的加权平均数
   背景是温度预测。
   关键公式：

   $$(1)v_{t}=\beta v_{t-1}+(1-\beta)\theta_{t}$$

   解释一下各个参数：

   • $v_{t}$：第t天的平均温度
   • $\beta$：超参数
   • $\theta_{t}$：第t天的温度

   

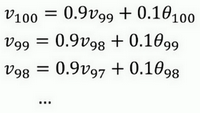
   公式里没看到指数啊？为什么就叫指数加权平均数了呢？

   其实公式(1)是一个递推关系式，指数就藏在里面：

   $$v_{100}=0.9v_{99}+0.1\theta_{100}=0.9(0.9v_{98}+0.1\theta_{99})+0.1\theta_{100}=0.1\theta_{100}+0.9\times 0.1\theta_{99}+0.9^{2}v_{98}=\cdots$$

   由此我们可以看到$v_{99}$的权重为0.9，而$v_{98}$的权重就降为了0.81，随着不断展开，v的距离越远，其权重的次幂就会越高，权重越低。

指数加权平均的偏差修正

帮助模型在早期获得更好的预测。

不用$v_{t}$，而用$\frac{v_{t}}{1-\beta^{t}}$，t就是现在的天数。举个具体例子，当t=2时，$1-\beta^{t}=1-0.98^{2}=0.0396$，因此对第二天温度的估测变成了$\frac{v_{2}}{0.0396}=\frac{0.0196 \theta_{1}+0.02 \theta_{2}}{0.0396}$，也就是$\theta_{1}$和$\theta_{2}$的加权平均数，并去除了偏差。你会发现随着增加，接近于0，所以当很大的时候，偏差修正几乎没有作用，因此当较大的时候，紫线基本和绿线重合了。

梯度下降优化算法

Momentum

动量梯度下降算法。原理：计算梯度的指数加权平均数，利用其更新权重。运行速度几乎总是快于标准梯度下降算法。

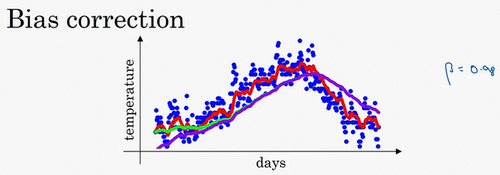
例如这个成本函数：

红点代表最小值，从蓝点开始梯度下降，为了使梯度下降的速度足够快，需要学习率尽可能高，但学习率太高，可能会偏离函数范围（紫色线），所以需要选择一个合理的学习率。

另一个看待问题的角度是，在纵轴上，你希望学习慢一点，因为你不想要这些摆动，但是在横轴上，你希望加快学习，你希望快速从左向右移，移向最小值，移向红点。使用动量梯度下降法，第t次迭代的过程中，使用mini-batch计算微分dW和db，套用指数加权平均数公式$v=\beta v+(1-\beta) \theta_{t}$，计算：

$$v_{d W}=\beta v_{d W}+(1-\beta) d W$$ $$v_{d b}=\beta v_{d b}+(1-\beta) d b$$

然后更新W和b：

$$W:=W-\alpha v_{d W}$$ $$b:=b-\alpha v_{d b}$$

在上几个导数中，你会发现这些纵轴上的摆动平均值接近于零，所以在纵轴方向，你希望放慢一点，平均过程中，正负数相互抵消，所以平均值接近于零。但在横轴方向，所有的微分都指向横轴方向，因此横轴方向的平均值仍然较大，因此用算法几次迭代后，你发现动量梯度下降法，最终纵轴方向的摆动变小了，横轴方向运动更快，因此你的算法走了一条更加直接的路径，在抵达最小值的路上减少了摆动。

Momentum更加适合碗状函数，Momentum项提供了一个W轴的初速度。

此时有两个超参数：$\alpha$、$\beta$。$\beta=0.9$是很好的鲁棒数（robust）

RMSprop

RMSprop算法，全称是root mean square prop算法，它也可以加速梯度下降。

RMSprop可以减缓b轴的摆动，同时加快，至少不是减缓x轴的速度。

套用指数加权平均数公式$v=\beta v+(1-\beta) \theta_{t}$，计算：

$$S_{d W}=\beta S_{d W}+(1-\beta) d W^{2}$$ $$S_{d b}=\beta S_{d b}+(1-\beta) d b^{2}$$

然后更新W和b：

$$W:=W-\alpha \frac{d W}{\sqrt{S_{d W}}}$$ $$b:=b-\alpha \frac{d b}{\sqrt{S_{d b}}}$$

原理：因为原来的函数斜率较大，db就比较大，而dW较小，所以在更新参数时，W会减去较小的一项，b会减去较大的一项，W下降的会慢一些，b会下降的快一些，所以就可以部分消除在b轴上的摆动

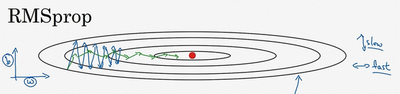
RMSprop的影响就是你的更新最后会变成这样（绿色线），纵轴方向上摆动较小，而横轴方向继续推进。还有个影响就是，你可以用一个更大学习率，然后加快学习，而无须在纵轴上垂直方向偏离。

为了确保数值稳定，在实际操练的时候，你要在分母上加上一个很小很小的$\varepsilon =10^{-8}$

Adam

Adam≈Momentum+RMSprop

1. 初始化：

   $$v_{d W}=0, \quad S_{d W}=0, \quad v_{d b}=0, \quad S_{d b}=0$$

2. 使用mini-batch计算：

   $$v_{d W}=\beta_{1} v_{d W}+\left(1-\beta_{1}\right) d W,\quad v_{d b}=\beta_{1} v_{d b}+\left(1-\beta_{1}\right) d b$$ $$S_{d W}=\beta_{2} S_{d W}+\left(1-\beta_{2}\right)(d W)^{2},\quad S_{d b}=\beta_{2} S_{d b}+\left(1-\beta_{2}\right)(d b)^{2}$$ $$v_{dW}^{corrected}=\frac{v_{dW}}{1-\beta_{1}^{t}},\quad v_{db}^{corrected}=\frac{v_{db}}{1-\beta_{1}^{t}}$$ $$S_{dW}^{corrected}=\frac{v_{dW}}{1-\beta_{2}^{t}},\quad S_{db}^{corrected}=\frac{v_{db}}{1-\beta_{2}^{t}}$$

3. 更新参数：

   $$W:=W-\alpha \frac{v_{dW}^{corrected}}{\sqrt{S_{dW}^{corrected}}+\varepsilon}$$ $$b:=b-\alpha \frac{v_{db}^{corrected}}{\sqrt{S_{db}^{corrected}}+\varepsilon}$$

超参数选择：

• $\alpha$：需要调试
• $\beta_{1}$：0.9
• $\beta_{2}$：0.999
• $\varepsilon$：$10^{-8}$

Adam代表的是Adaptive Moment Estimation，$\beta_{1}$用于计算这个微分（$dW$），叫做第一矩，$\beta_{2}$用来计算平方数的指数加权平均数（$(dW)^{2}$），叫做第二矩，所以Adam的名字由此而来。

Adam由于有更多的参数，在迭代过程中会占用更多的显存。

学习率衰减

对应《深度学习入门》中的AdaGrad

学习率为固定值时，使用mini-batch训练模型有时会有一些噪声，这使得梯度下降时，最终会在最小值附近较大的区域内摆动，而不会收敛到极小值。而使用学习率衰减，可以使学习率在迭代的过程中逐渐下降，使得梯度下降时，能够在最小值附近较小的区域内摆动，甚至可以直接收敛到极小值。

1. 线性衰减：

   $$\alpha = \frac{1}{1+decayrate*epochnum}\alpha_{0}$$

   decay-rate称为衰减率，epoch-num为代数，$\alpha_{0}$为初始学习率

2. 指数衰减：

   $$\alpha=\frac{k}{\sqrt{epochnum}}\alpha_{0},或\alpha=\frac{k}{\sqrt{t}}\alpha_{0}$$

   t为mini-batch

3. 离散下降：
   在某个步骤有某个学习率之后，学习率减少一半；一会儿减少一半，一会儿又一半。