4.深度学习实用层面

训练、验证、测试集

1. 如果数据集较小，可将所有数据按照3:1:1的比例分配训练集、验证集和测试集；
   或7:3的比例分配训练集和测试集（无验证集）
2. 如果数据集较大
   • 百万级别：训练集 : 验证集 : 测试集 = 98% : 1% : 1%
   • 过百万级别：训练集 : 验证集 : 测试集 = 99.5% : 0.25% : 0.25%（或99.5% : 0.4% : 0.1%）

偏差、方差

知乎回答：Jason Gu
Understanding the Bias-Variance Tradeoff

偏差：描述的是预测值（估计值）的期望与真实值之间的差距。偏差越大，越偏离真实数据，如下图第二行所示。

方差：描述的是预测值的变化范围，离散程度，也就是离其期望值的距离。方差越大，数据的分布越分散，如下图右列所示。

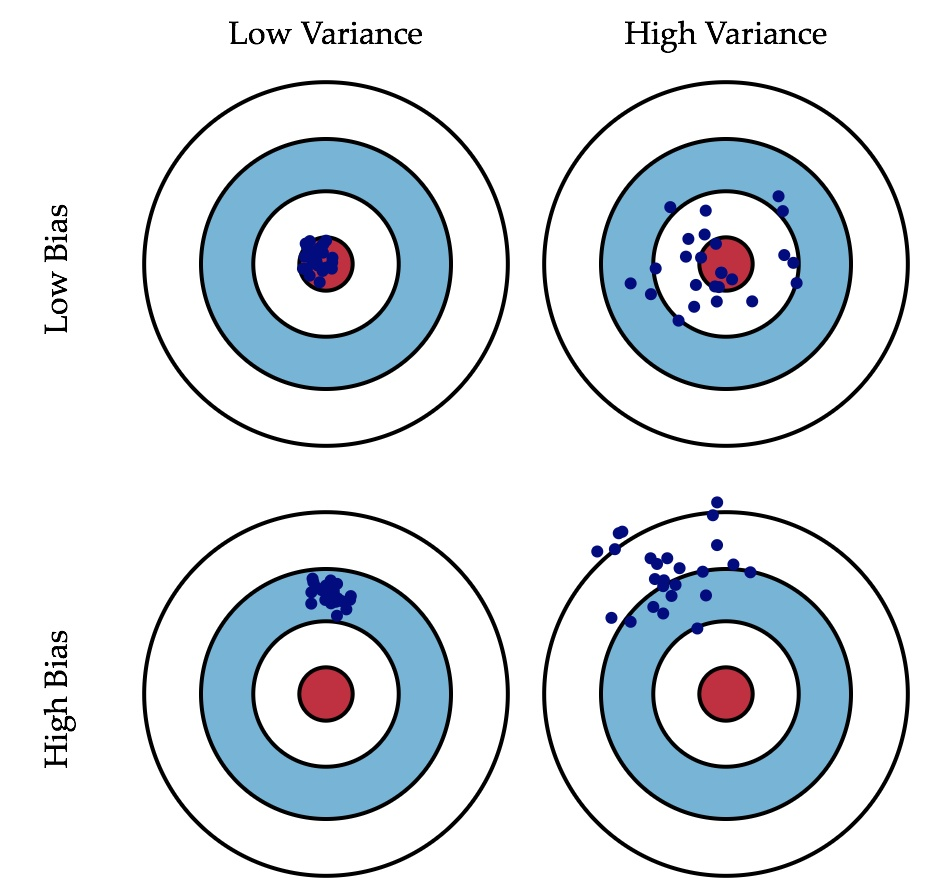
举例说明：

Train set error	1%	15%	15%	0.5%
Dev set error	11%	16%	30%	1%
	高方差	高偏差	高偏差&高方差	低偏差&低方差

正则化

作用：减少过拟合

• L1范数： $$L1=\|w\|_{1}$$
• L2范数（更加常用）： $$L2=\|w\|_{2}^{2}$$

正则化：

• L1正则化：

  $$J(w, b)=\frac{1}{m} \sum_{i=1}^{m} L\left(\hat{y}^{(i)}, y^{(i)}\right) + \frac{\lambda}{m}\|\omega\|_{1}$$

• L2正则化：

  $$J(w, b)=\frac{1}{m} \sum_{i=1}^{m} L\left(\hat{y}^{(i)}, y^{(i)}\right) + \frac{\lambda}{2 m}\|\omega\|_{2}^{2}$$

在神经网络中实现正则化

$$(1)J(w^{[1]},b^{[1]},...,w^{[L]},b^{[L]})=\frac{1}{m} \sum_{i=1}^{m} L\left(\hat{y}^{(i)}, y^{(i)}\right)+\frac{\lambda}{2 m}\sum_{l=1}^{L}\|W^{[l]}\|_{F}^{2}$$

(1)神经网络的成本函数包含$W^{[1]},b^{[1]}$到$W^{[l]},b^{[l]}$所有参数，$L$为神经网络层数。成本函数等于m个训练样本损失函数的总和的平均值，正则项为：

$$\frac{\lambda}{2 m}\sum_{l=1}^{L}\|W^{[l]}\|_{F}^{2}$$

矩阵中所有元素的平方和为：

$$\|W^{[l]}\|^{2}$$ $$(2)\|W^{[l]}\|_{F}^{2}=\sum_{i=1}^{n^{[l-1]}} \sum_{j=1}^{n^{[l]}}(w_{ij})^{2}$$

(2)第一个求和符号其值$i$从1到$n^{[l-1]}$，第二个求和符号其值$j$从1到$n^{[l]}$，因为$W$是一个$n^{[l]}×n^{[l-1]}$的多维矩阵，$n^{[l]}$表示$l$层单元的数量，$n^{[l-1]}$表示$l-1$层单元的数量。

使用范数实现梯度下降

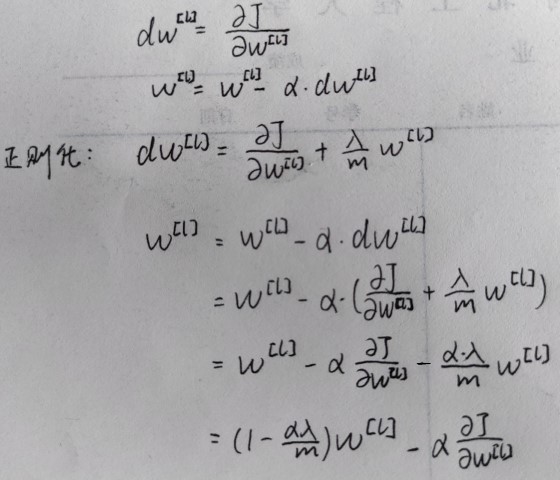
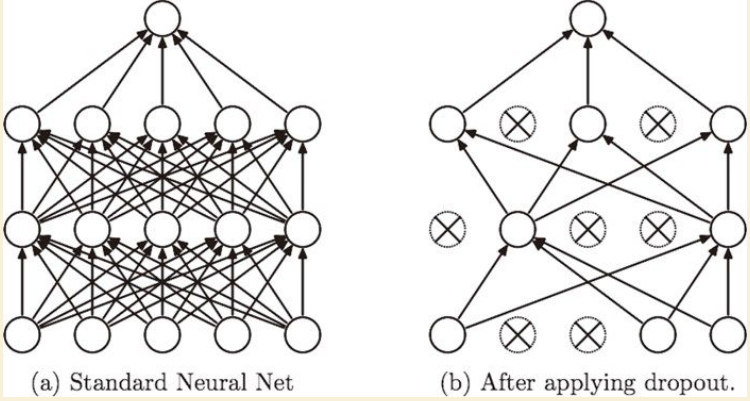
Dropout正则化

随机删除一些神经网络中的神经元及从该神经元进出的连线。

《深度学习入门》

集成学习：让多个模型单独学习，推理时再取多个模型的输出平均值，可提高神经网络识别精度。
集成学习与Dropout有密切的联系，可以将Dropout理解为，通过在学习过程中随机删除神经元，从而每一次都让不同的模型进行学习。推理时通过对神经元的输出乘以删除比例，可以取得模型的平均值。可以理解为，Dropout将集成学习的效果（模拟地）通过一个网络实现了。

实施Dropout

正向传播

对于已经被激活的矩阵A1：

A1 = [[ 0.46544685,  0.34576201, -0.00239743,  0.34576201, -0.22172585],
      [ 0.57248826,  0.42527883, -0.00294878,  0.42527883, -0.27271738],
      [ 0.45465921,  0.3377483,  -0.00234186,  0.3377483,  -0.21658692]]
A1 = np.array(A1)

keep_prob表示保留神经元的概率

1. 初始化一个mask：

   mask = np.random.randn(A1.shape[0], A1.shape[1])
   mask = mask < keep_prob  # mask会变成一个布尔型数组

2. 使用mask对A1进行遮罩：

   A1 = np.multiply(A1, mask)

3. 为了修正期望值，需要除以keep_prob：

   A1 = A1 / keep_prob

   ---

   这里说一点自己的理解：这个mask翻译成遮罩就非常灵性，可以想象到有一个跟A1一样大的板子叫mask，遮挡在A1上，值为True的地方是个洞，就可以使A1中的数字露出来，而每次这些洞的位置都是随机的。

反向传播

与正向传播非常类似，只需要两步，正向传播与反向传播需要使用相同的mask，所以反向传播时，要将正向传播所使用的mask作为参数，传递给反向传播的函数。

假设只有2层的神经网络：

1. 使用mask对dA2进行遮罩：

   dA2 = np.multiply(mask,dA2)

2. 修正期望值：

   dA2 = dA2 / keep_prob

理解dropout

不依赖于某一个特定的特征，所以必须将权重传播出去。因为神经元可能会被随时删除，通过传播权重，给其他输入增加一点权重，从而达到压缩权重的平方范数的效果，这和L2正则化的效果类似。

每一层的keep_prob可以不同，如果担心某些层比其他层更容易发生过拟合，可以将keep_prob设置地更小；缺点是为了使用交叉验证，需要搜索更多的参数。另一种方案是在一些层上应用dropout，而有些层不用dropout，应用dropout的层只含有一个超级参数，就是keep-prob。

在计算机视觉领域，dropout很常用，因为输入的像素点很多，但要牢记dropout只是一种正则化方法。dropout的缺点是代价函数J不明确，每次迭代都会随机移除一些节点，导致无法确定梯度下降的性能。这导致我们所优化的代价函数失去了其应有的意义。

其他正则化方法

数据扩增

如果采集新的数据比较困难，可以通过对图片的基本操作：旋转、反转、裁剪等增加训练集，虽然这种方式不如新数据的效果好，但基本没有额外花销。从而以近乎零成本正则化数据集，减少过拟合。

early stopping

在模型还没有发生过拟合（或者过拟合较低）的情况下，提早结束神经网络的训练过程。

优点：

• 防止过拟合
• 模型训练的代价较低

缺点：（提早结束训练，性能不太好，具体表现如下）

• 代价函数J没有尽可能降到最低

• 模型的方差可能也没有降到最低

  ---

  通过一种办法同时降低偏差与方差的方法显然是不太现实的。

early stopping适用于对模型要求不高的情况，但我认为深度学习没有最好，只有更好，我们只会追求越来越好的模型，而不是在某一个地方驻足，这显然是一个”治标不治本“的办法。

归一化输入

先说说什么是归一化：

让所有数据映射到(0,1)中的方法叫做归一化。公式为：

$$x^{\prime}=\frac{x-\min (x)}{\max (x)-\min (x)}$$

这里的说法其实不太准确，引用知乎答者的回答：

gokenu

正在做相关的作业,我来做一些小小的努力,不让概念太混乱

查看了@龚焱的回答中提到的wiki 大致意思是归一化和标准化都属于四种Feature scaling(特征缩放),这四种分别是

1. Rescaling (min-max normalization) 有时简称normalization(有点坑)
2. Mean normalization
3. Standardization(Z-score normalization)
4. Scaling to unit length

对比了一下其它回答和一些博客,一般把第一种叫做归一化,第三种叫做标准化.不是很清楚是怎么翻译的.正则化的英文应该是Regularization,有些博客把这也弄混了.正则化是完全不同的事情了.

然后关于在ML里面是用第一个好还是第三个好,感觉大家都讨论的很激烈.有的认为取决于你的数据的特点(是否稀疏),有的认为取决于数据是否有明确的界限. 个人不太赞同只有归一化让椭圆变成了圆的想法,在我的梯度下降中,两种都加速得挺好…

---

归一化输入分为两步：

1. 零均值化
2. 归一化方差

使用二维数据说明什么是归一化输入：

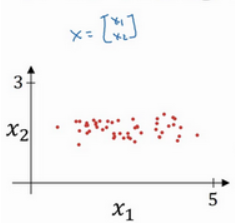
第一步是零均值化：

$$\mu=\frac{1}{m} \sum_{i=1}^{m} x^{(i)}$$ $$x:=x-\mu$$

意思是移动训练集，直到它完成零均值化。零均值化后：

深度学习笔记

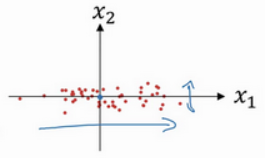
这里应该套用的是

$$x^{\prime}=\frac{x-\operatorname{mean}(x)}{\sigma}$$

只不过经过步骤一，mean变成0了，$\sigma$变成$\sigma^{2}$了

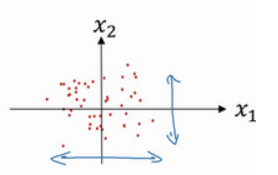
以上只是解释了归一化输入的两个步骤，接下来解释为什么要归一化输入。

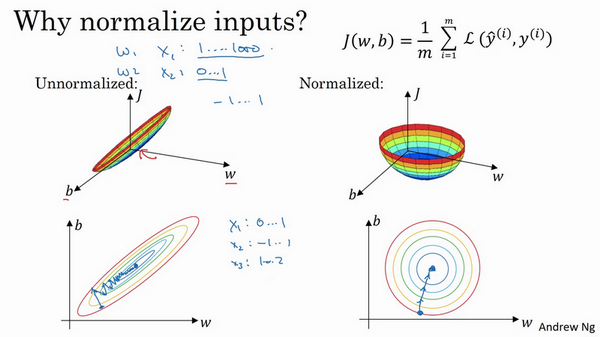
吴恩达老师的这张ppt非常直观。

使用归一化输入后，代价函数看起来更加对称，无论从什么位置开始，梯度下降都会更快，可以在梯度下降中使用更大的步长，从而提高学习的速度。

梯度消失/梯度爆炸

训练深层次的神经网络时，导数（梯度）会变得非常大或非常小，甚至是指数级变小，这使训练难度变大。

假设要训练的神经网络长这样：

其中激活函数

$$g(z)=z,b^{[l]}=0$$

则

$$\hat{y}=W^{[l]}W^{[l-1]}W^{[l-2]}\cdot \cdot \cdot W^{[3]}W^{[2]}W^{[1]}x$$

又

$$z^{[1]}=W^{[1]}x,a^{[1]}=g(z^{[1]})=z^{[1]}$$

则

$$\hat{y}=W^{[l]}a^{[l-1]}x$$

假设

$$W^{[l]}= \begin{bmatrix} 1.5 & 0\\ 0 & 1.5 \end{bmatrix}$$

则

$$\hat{y}=W^{[l]} \begin{bmatrix} 1.5 & 0\\ 0 & 1.5 \end{bmatrix}^{[l-1]}x$$

此时，指数$[l-1]$就会导致梯度爆炸；如果

$$W^{[l]}= \begin{bmatrix} 0.5 & 0\\ 0 & 0.5 \end{bmatrix}$$

此时，指数$[l-1]$就会导致梯度消失。

权重初始化

为了解决梯度消失/梯度爆炸，虽然不能彻底解决，但很有效。

以单个神经元为例：

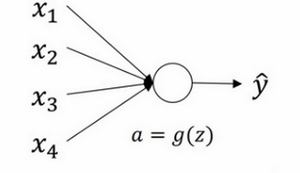
有4个输入特征，经过$a=g(z)$处理，最后得到$\hat{y}$。稍后讲深度网络时，这些输入表示为$a^{[l]}$，暂时我们用$x$表示。

• 如果使用Relu作为激活函数，则用公式$\sqrt{\frac{2}{n^{[l-1]}}}$
• 如果使用tanh作为激活函数，则用公式$\sqrt{\frac{1}{n^{[l-1]}}}$

吴恩达老师说：

意思是作为超参数时，调整的优先级较低。

梯度检验

梯度检验是为了保证backprop正确实施，其对整个模型的训练没有作用，为了实现梯度检验，需要先了解梯度的数值逼近

梯度的数值逼近

这里老师就是讲了个导数的第二种定义（双边误差）：

$$\left.f^{\prime} (\theta\right)=\frac{f(\theta + \varepsilon)-f(\theta-\varepsilon)}{2 \varepsilon}$$

使用双边误差而不使用单边误差是因为更加精确。

比较好理解，不多赘述了

梯度检验

将所有$W$和$b$转换为向量，做连接运算，从而组合成一个巨大向量$\theta$，代价函数$J$是所有$W$和$b$的函数，即$J$是$\theta$的函数：

$$J\left(W^{[1]}, b^{[1]}, \ldots, W^{[l]}, b^{[l]}\right)=J(\theta)$$

将所有$dW$和$db$转换为矩阵，注意$dW$和$W$、$db$和$b$具有相同的维度。同样地，经过转换与连接操作后，得到一个巨大向量$d\theta$，它与$\theta$具有相同的维度，问题是：$d\theta$和代价函数$J$的梯度（坡度）有什么关系？

首先，我们要清楚$J$是超参数$\theta$的一个函数，你也可以将$J$展开为$J\left(\theta_{1}, \theta_{2}, \theta_{3}, \ldots \ldots\right)$，不论超级参数向量$\theta$的维度是多少，为了实施梯度检验，要做的就是循环执行，从而对每个$\theta$也就是对每个组成元素计算$d \theta_{\text {approx }}[i]$的值，我使用双边误差，也就是：

$$d \theta_{\text {approx }}[i]=\frac{J\left(\theta_{1}, \theta_{2}, \ldots \theta_{i}+\varepsilon, \ldots\right)-J\left(\theta_{1}, \theta_{2}, \ldots \theta_{i}-\varepsilon, \ldots\right)}{2 \varepsilon}$$

只对$\theta_{i}$增加$\varepsilon$，其它项保持不变，使用的是双边误差，对另一边做同样的操作，减去$\varepsilon$，其它项全都保持不变。

$d \theta_{\text {approx }}[i]$应该逼近$d \theta_{\text {approx }}$，$d\theta[i]$是代价函数的偏导数，然后需要对i的每个值都执行这个运算，最后得到两个向量，得到$d\theta$的逼近值$d \theta_{\text {approx }}$，它与$d\theta$具有相同维度，它们两个与$\theta$具有相同维度，要做的就是验证这些向量是否彼此接近。

如何衡量彼此接近？

计算以下方程式：

$$\frac{\| d \theta_{approx}-d \theta \|_{2}}{\left\|d \theta_{approx} \right\|_{2}+\|d \theta\|_{2}}$$

上式的值为：

• $10^{-7}$：很好
• $10^{-5}$：注意，可能会有bug
• $10^{-3}$：有bug，需要检查所有$\theta$，看是否有一个具体的$i$值，使得$d \theta_{\text {approx }}[i]$ 与 $d \theta[i]$大不相同，并用它来追踪一些求导计算是否正确

梯度检验的注意事项

1. 梯度检验仅用于调试，不能用于训练

2. 如果算法的梯度检验失败，要检查所有项，尝试找到bug

3. 在实施梯度检验时，如果使用正则化，请注意正则项。如果代价函数

   $$J(\theta)=\frac{1}{m} \sum L\left(\hat{y}^{(i)}, y^{(i)}\right)+\frac{\lambda}{2 m} \sum\left\|W^{[l]}\right\|^{2}$$

   这就是代价函数$J$的定义，$d\theta$等于与$\theta$相关的$J$函数的梯度，包括这个正则项，记住一定要包括这个正则项。

4. 梯度检验不能与dropout一起使用，如有需要，则先将dropout的keep_prob设为1，使用梯度检验检查无误后，再调整keep_prob

5.