3.浅层神经网络

发表于 | 分类于
字数统计: 2k | 阅读时长 ≈ 8

神经网络概览及表示

个人认为，这节只需要搞懂两个问题：

单个神经元的作用

graph LR
x1-->B((N))
x2-->B((N))
x3-->B((N))
B-->y

对于一个这样的神经元N，他要做的计算主要是上一章的$\hat{y}=w^{T} x+b$和$a=sigmoid(z)$，并输出损失函数L的值，如下图所示：

graph LR

A["x"]-->B[z=wx+b]
w["w"]-->B
b["b"]-->B
B-->C["a=sigmoid(z)"]
C-->D["L"]

层与层的信号传递

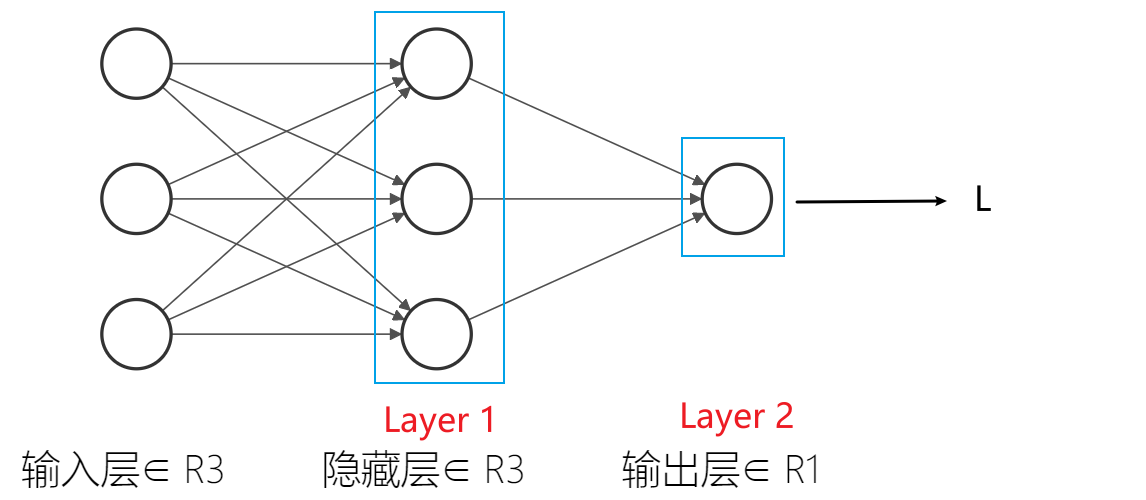
d0KBrQ.png

对于这样一个简单的双层网络（输入层不被视为标准层），层与层之间是如何进行信号传输的呢？

对于Layer 1，使用以下公式进行计算：

这里对参数进行说明：

  • $x$：输入样本
  • $W^{[1]}$：参数$w$矩阵
  • $b^{[1]}$：参数$b$矩阵

对于Layer 2，上一层的输出$a^{[1]}$为这一层的输入：

参数说明同上，不再赘述。此时输出结果$a^{[2]}$即为整个神经网络的输出结果。这就完成了一次神经网络的正向传播。

这里对这个神经网络进行简单的说明：对于外界，隐藏层Layer 1与Layer 2不可见，之所谓“隐藏”。

那反向传播呢？

类似于这样：

graph RL
L[dL]-->a["da"]
a-->z["dz"]
z-->x[x]
z-->w[dW]
z-->b[db]

使用如下公式计算：

计算一个神经网络的输出

这一节主要了解神经网络的输出是如何计算的。

由上节可知，单个神经元的计算为：

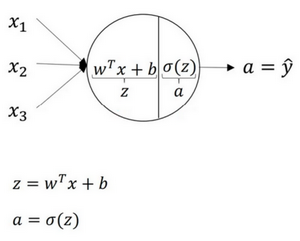
d01NwQ.png

在双层神经网络中为：

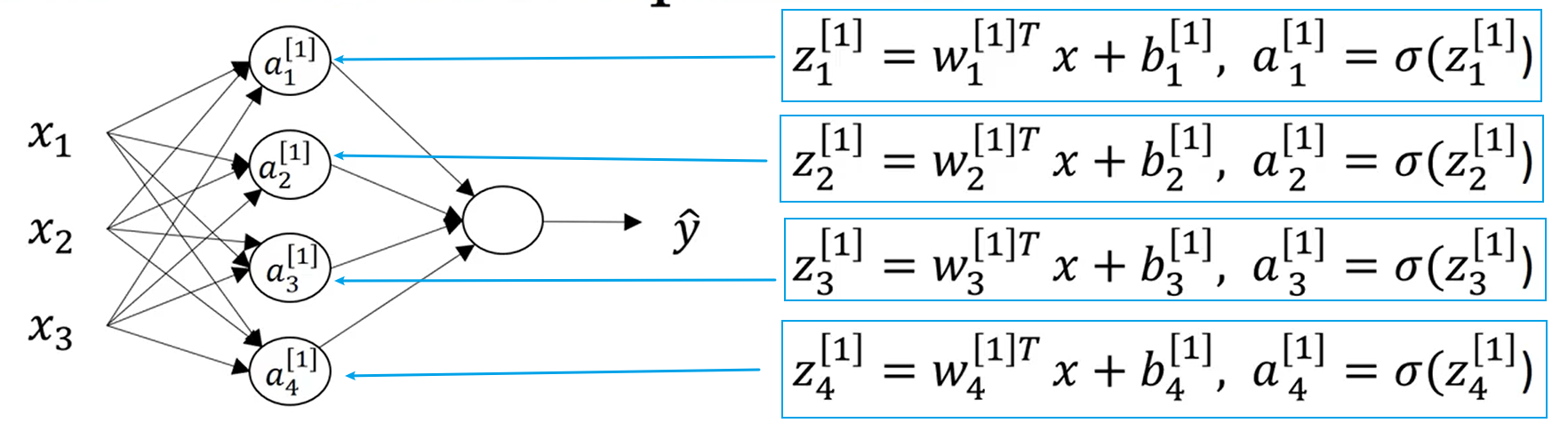
d01xpt.png

使用for循环计算很低效，因此采用向量法计算：

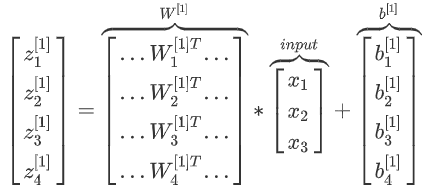
d03WDS.png

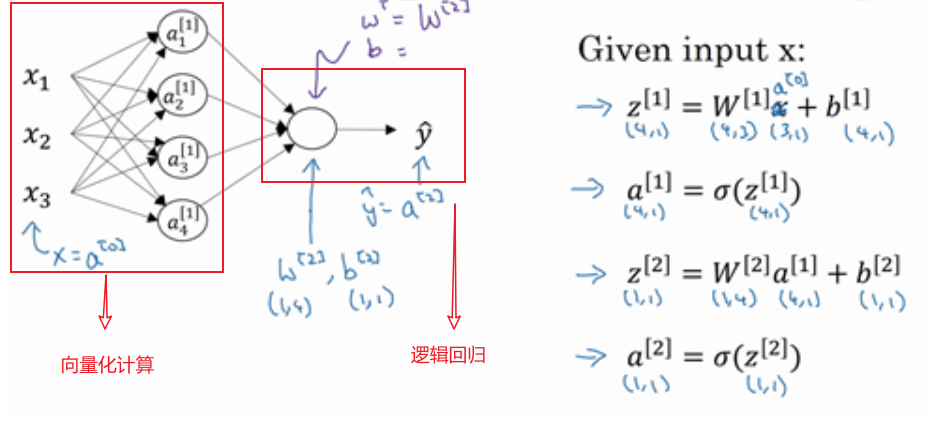
d08kDO.png

多样本向量化

上节讨论了单一样本的训练，这节针对多样本训练。

针对单一样本，使用以下四个函数可以计算出$\hat{y}$：

将这四个函数应用于m个样本上，就需要重复以上四个函数m次：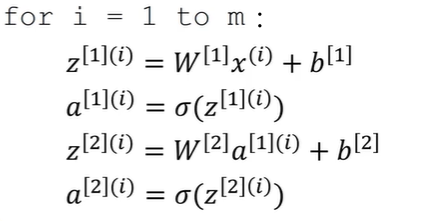
d0LAOJ.png

注：$a^{[2](i)},(i)$是指第$i$个训练样本而$[2]$是指第二层。

将以上公式向量化：

同理可求得$Z^{[2]}$，$A^{[2]}$：

水平索引（纵列）针对训练样本，垂直索引（横列）针对神经网络的节点（一行代表一个Layer）

向量化的解释

先手动对几个样本进行向前传播：

为了简便理解，先$b^{[1]}$舍去，之后可利用python的广播机制再加回来。现在$W^{[1]}$是一个矩阵，$x^{(1)}, x^{(2)}, x^{(3)}$都是列向量，矩阵乘以列向量得到列向量，表示如下：

吴恩达老师很细心的用不同的颜色表示不同的样本向量，及其对应的输出。所以从上式中可以看出，当加入更多样本时，只需向矩阵$X$中加入更多列。

激活函数

单个神经元中，实现非线性映射的函数。

激活函数分类

sigmoid函数

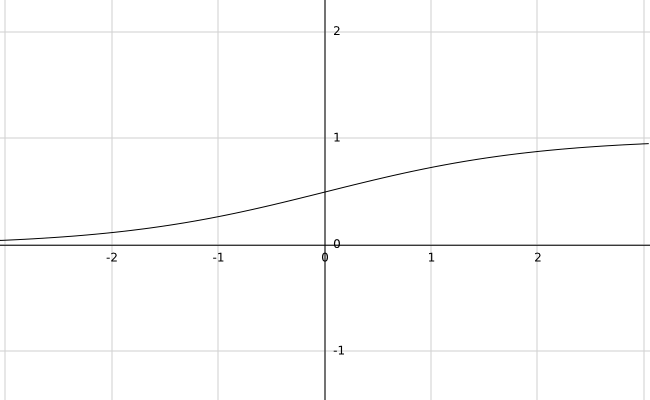
d6RGMd.png

只适用于逻辑回归模型，不常用。

tanh函数

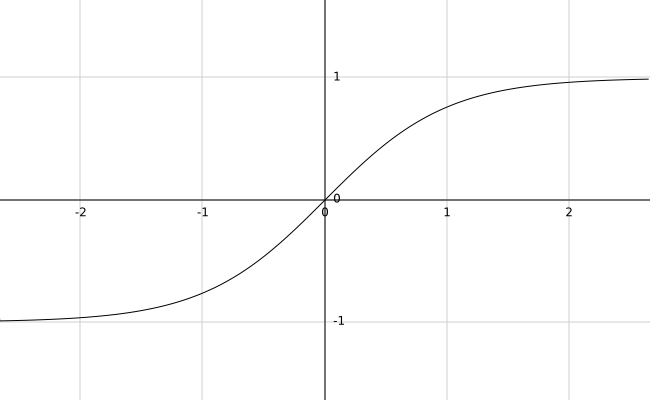
d65fxS.png

比sigmoid函数性能更好，更加适用于多场景，更常用。

sigmoid函数和tanh函数两者共同的缺点是，在$z$的绝对值特别大时，导数的梯度或者函数的斜率会变得特别小，最后就会接近于0，导致梯度下降的速度降低。

ReLU

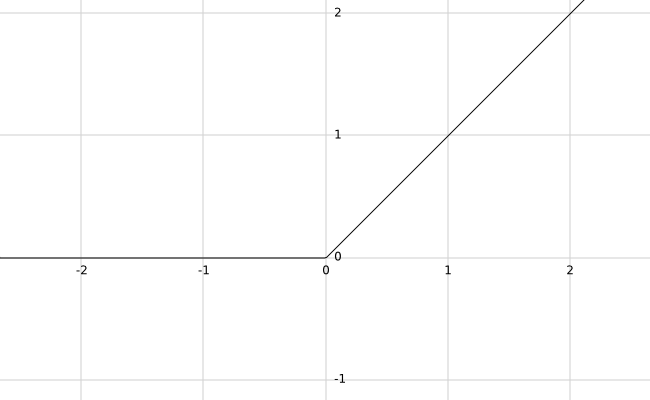
d6T1KS.png

激活函数的默认选择，可以解决sigmoid函数和tanh函数两者共同的缺点。

Leaky ReLu

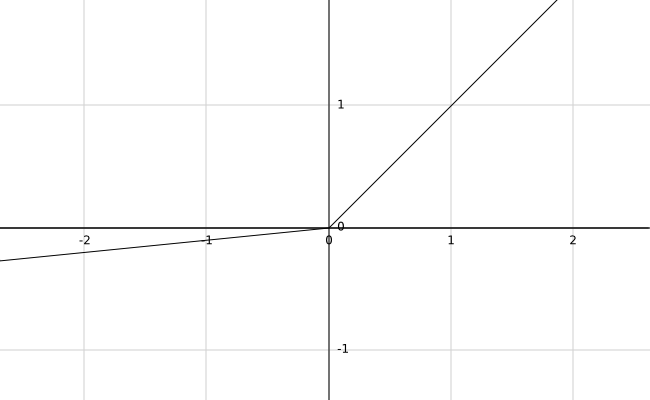
d6bfx0.png

这个函数通常比Relu激活函数效果要好。0.01是学习函数的一个参数，也可以设置为别的。

ReLU与Leaky ReLu共同的优点：

摘自深度学习笔记，我也不是很理解这里。

  • 在$z$的区间变动很大的情况下，激活函数的导数或者激活函数的斜率都会远大于0，在程序实现就是一个if-else语句，而sigmoid函数需要进行浮点四则运算，在实践中，使用ReLu激活函数神经网络通常会比使用sigmoid或者tanh激活函数学习的更快。
  • sigmoid和tanh函数的导数在正负饱和区的梯度都会接近于0，这会造成梯度弥散，而Relu和Leaky ReLu函数大于0部分都为常数，不会产生梯度弥散现象。(同时应该注意到的是，Relu进入负半区的时候，梯度为0，神经元此时不会训练，产生所谓的稀疏性，而Leaky ReLu不会有这问题)

结论

  1. sigmoid激活函数：仅适用于二分类
  2. tanh激活函数：tanh是非常优秀的，几乎适合所有场合。
  3. ReLu激活函数：最常用的默认函数，如果不确定用哪个激活函数，就使用ReLu或者Leaky ReLu。

为什么需要非线性激活函数

线性激活函数会使预测值与输入呈现线性关系，而失去了多层神经网络迭代参数的意义。

只有机器学习中的回归问题可以用到线性函数。

激活函数的导数

  1. sigmoid

  2. tanh

  3. ReLU

  4. Leaky ReLU

神经网络的梯度下降

dWErTS.png

随机初始化

不能把参数或权重都设置为0，否则反向传播会失效，因为每层的神经元计算的函数将会一模一样。

可以把$b$初始化为0，因为只要随机初始化$W$就会有不同的隐藏单元计算不同的函数。