621.任务调度器

发表于 | 分类于
字数统计: 1k | 阅读时长 ≈ 3

一、题目描述

给定一个用字符数组表示的 CPU 需要执行的任务列表。其中包含使用大写的 A - Z 字母表示的26 种不同种类的任务。任务可以以任意顺序执行，并且每个任务都可以在 1 个单位时间内执行完。CPU 在任何一个单位时间内都可以执行一个任务，或者在待命状态。

然而，两个相同种类的任务之间必须有长度为 n 的冷却时间，因此至少有连续 n 个单位时间内 CPU 在执行不同的任务，或者在待命状态。

你需要计算完成所有任务所需要的最短时间。

示例 1：

1
2
3
输入: tasks = ["A","A","A","B","B","B"], n = 2
输出: 8
执行顺序: A -> B -> (待命) -> A -> B -> (待命) -> A -> B.

注：

  1. 任务的总个数为 [1, 10000]。
  2. n 的取值范围为 [0, 100]。

二、题解

1.算法描述

2.个人分析

我不是很理解，这里就把官解贴在这里吧🙃

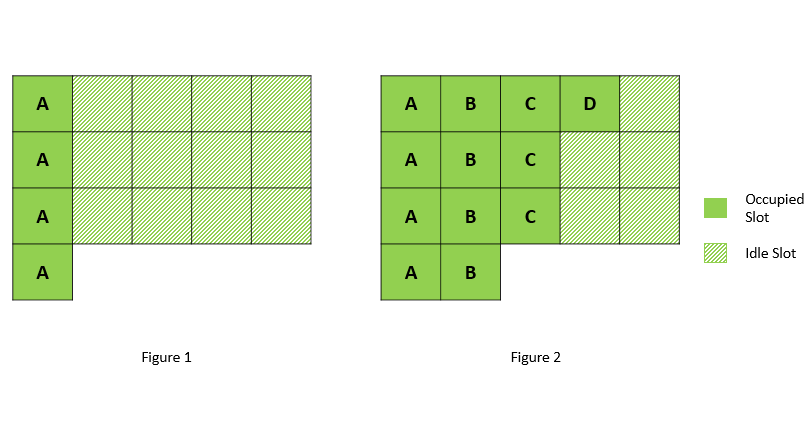
在前两种方法中，我们了解到应当尽早安排出现次数较多的任务。我们假设 A 为出现次数最多的任务，假设其出现了 p 次，考虑到冷却时间，那么执行完所有任务的时间至少为 (p - 1) (n + 1) + 1。我们把这个过程形象化地用图 1 表现出，可以发现，CPU 产生了 (p - 1) n 个空闲时间，只有 p 个时间是在工作的。

621_Task_Scheduler_new.png

因此我们应当考虑把剩余的任务安排到这些空闲时间里，我们仍然按照这些任务的出现次序，从大到小进行安排，会有下面三种情况：

  • 某个任务和 A 出现的次数相同，例如图 2 中的任务 B。此时我们只能让 B 占据 p - 1 个空闲时间，而在非空闲时间里额外安排一个时间给 B 执行；

  • 某个任务比 A 出现的次数少 1，例如图 2 中的任务 C。此时我们可以让 C 占据 p - 1 个空闲时间，就可以全部执行完；

  • 某个任务比 A 出现的次数少 2 或更多，例如图 2 中的任务 D。此时我们可以按照列优先的顺序，将 D 填入空闲时间中。因为 D 出现的次数少于 p - 1，因此无论从哪个位置开始按照列优先的顺序放置，都可以保证相邻的两个 D 之间满足冷却时间的要求。

在将所有的任务安排完成后，如果仍然有剩余的空闲时间，那么答案即为（任务的总数 + 剩余的空闲时间）；如果在安排某一个任务时，遇到了剩余的空闲时间不够的情况，那么答案一定就等于任务的总数。这是因为我们可以将空闲时间增加虚拟的一列，继续安排任务。如果不考虑这些虚拟的列，在原本空闲时间对应的那些列中的任务是可以按照要求顺序执行的，而增加了这些虚拟的列后，两个相邻的相同任务的间隔不可能减少，并且虚拟的列中的任务也满足冷却时间的要求，因此仍然顺序执行并跳过虚拟的列中剩余的“空闲时间”一定是可行的。

3.代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int cmp(const void *a, const void *b)
{
    return *(int *)a - *(int *)b;
}
int min(int a, int b)
{
    return a > b ? b : a;
}
int leastInterval(char *tasks, int tasksSize, int n)
{
    int map[26];
    memset(map, 0, 26 * sizeof(int));
    for (int i = 0; i < tasksSize; i++)
        map[tasks[i] - 'A']++;
    qsort(map, 26, sizeof(int), cmp);
    int max_val = map[25] - 1, idle_slots = max_val * n;
    for (int i = 24; i >= 0 && map[i] > 0; i--)
        idle_slots -= min(map[i], max_val);
    return idle_slots > 0 ? idle_slots + tasksSize : tasksSize;
}