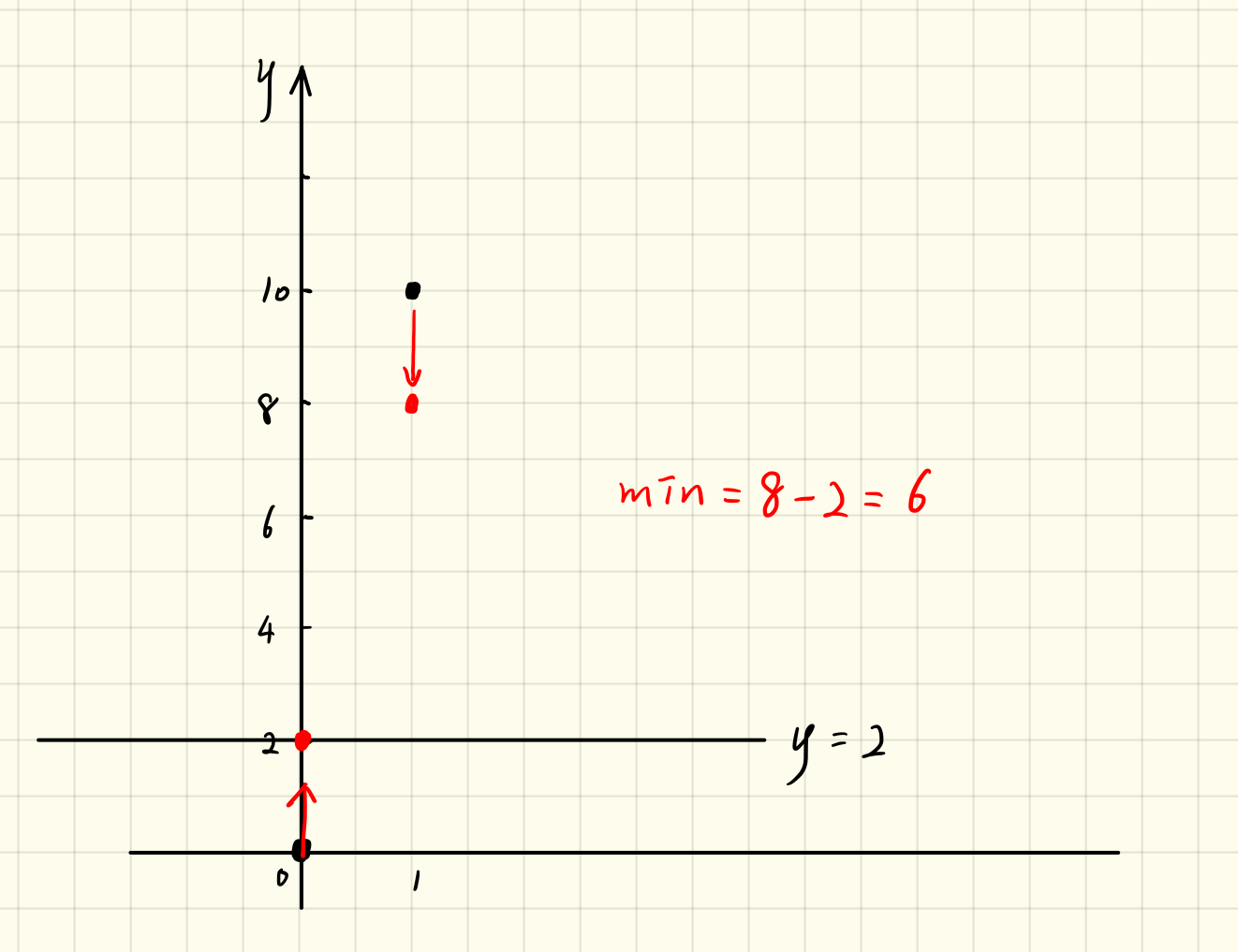908.最小差值 I

发表于 | 分类于
字数统计: 391 | 阅读时长 ≈ 1

一、题目描述

给定一个整数数组 A，对于每个整数 A[i]，我们可以选择任意 x 满足 -K <= x <= K，并将 x 加到 A[i] 中。

在此过程之后，我们得到一些数组 B。

返回 B 的最大值和 B 的最小值之间可能存在的最小差值。

示例 1：

1
2
3
输入：A = [1], K = 0
输出：0
解释：B = [1]

示例 2：

1
2
3
输入：A = [0,10], K = 2
输出：6
解释：B = [2,8]

示例 3：

1
2
3
输入：A = [1,3,6], K = 3
输出：0
解释：B = [3,3,3] 或 B = [4,4,4]

提示：

  1. 1 <= A.length <= 10000
  2. 0 <= A[i] <= 10000
  3. 0 <= K <= 10000

二、题解

1.算法描述

  • 遍历数组

2.个人分析

  • 找出数组中的最大值和最小值，所求的数应该是(max - min) > 2 * K ? max - min - 2 * K : 0;

3.代码

1
2
3
4
5
6
7
8
9
10
11
int smallestRangeI(int *A, int ASize, int K)
{
    int min = A[0], max = A[0];
    int i;
    for (i = 0; i < ASize; i++)
    {
        min = A[i] > min ? min : A[i];
        max = A[i] < max ? max : A[i];
    }
    return (max - min) > 2 * K ? max - min - 2 * K : 0;
}

三、PS

这里再多说两句：

首先，这道题描述的不是很清楚。

转述：给定一个整数K，使数组中的数加上[-K, K]的数后的差值最小。

后来我就想，这其实就是一道线性规划的题嘛。

比如说题目中的测试用例：

1
2
3
输入：A = [0,10], K = 2
输出：6
解释：B = [2,8]

就是让散列点都向y=2靠近：

3DC81E16CD0CEB3016C92FF18EC45BBE.png